Find charge in each capacitor:
To find the charge in each capacitor in the given circuit, we will follow these steps:
1. Identify the Capacitors and Their Values:
Let's assume we have four capacitors with capacitances C1=6μF, C2=3μF, C3=4μF, and C4=8μF.
2. Set Up the Charge Relationships:
In steady state, we can assume the charges on the capacitors are related. Let's denote the charge on capacitor C1 as Q1, on C2 as Q2, on C3 as Q3, and on C4 as Q4.
From the problem, we can write:
Q16+Q13=Q12(Equation 1)
3. Apply Kirchhoff's Voltage Law (KVL):
For the loop involving C2 and C3, we can set up another equation:
Q34=Q22(Equation 2)
4. Relate the Charges:
From Equation 1, we can express Q2 in terms of Q1:
Q2=Q1(from Equation 1)
From Equation 2, we can express Q3 in terms of Q1:
Q3=2Q1(from Equation 2)
5. Total Charge Conservation:
Since the total charge in the system must be conserved, we can write:
Q1+Q2+Q3=Q4
Substituting the expressions for Q2 and Q3:
Q1+Q1+2Q1=Q4⟹4Q1=Q4
6. Calculate Q4:
Given that the voltage across the battery is 8V, we can find Q4:
Q4=Ceffective×V
The effective capacitance Ceffective can be calculated as:
Ceffective=QV=32μC8V=4μF
Thus, Q4=32μC.
7. Calculate Charges on Other Capacitors:
Now we can find Q1:
Q1=Q44=32μC4=8μC
Since Q2=Q1:
Q2=8μC
And for Q3:
Q3=2Q1=2×8μC=16μC
Final Answers:
- Q1=8μC
- Q2=8μC
- Q3=16μC
- Q4=32μC
Let's assume we have four capacitors with capacitances C1=6μF, C2=3μF, C3=4μF, and C4=8μF.
In steady state, we can assume the charges on the capacitors are related. Let's denote the charge on capacitor C1 as Q1, on C2 as Q2, on C3 as Q3, and on C4 as Q4.
From the problem, we can write:
Q16+Q13=Q12(Equation 1)
For the loop involving C2 and C3, we can set up another equation:
Q34=Q22(Equation 2)
From Equation 1, we can express Q2 in terms of Q1:
Q2=Q1(from Equation 1)
From Equation 2, we can express Q3 in terms of Q1:
Q3=2Q1(from Equation 2)
Since the total charge in the system must be conserved, we can write:
Q1+Q2+Q3=Q4
Substituting the expressions for Q2 and Q3:
Q1+Q1+2Q1=Q4⟹4Q1=Q4
Given that the voltage across the battery is 8V, we can find Q4:
Q4=Ceffective×V
The effective capacitance Ceffective can be calculated as:
Ceffective=QV=32μC8V=4μF
Thus, Q4=32μC.
Now we can find Q1:
Q1=Q44=32μC4=8μC
Since Q2=Q1:
Q2=8μC
And for Q3:
Q3=2Q1=2×8μC=16μC
- Q1=8μC
- Q2=8μC
- Q3=16μC
- Q4=32μC
Topper's Solved these Questions
Similar Questions
Find charge on each capacitor

View SolutionFind charge on each capacitor and potential difference across each capacitor .

View SolutionIn the circuit shown, r=4Ω, C=2μF
(a) Find the current coming out of the battery just after the switch is closed.
(b) Find charge on each capacitor in the steady state condition.

View SolutionIn the circuit shown, r=4Ω,C=2μF
(a) Find the current coming out of the battery just after the switch is closed
(b) Find charge on each capacitor in the steady state condition
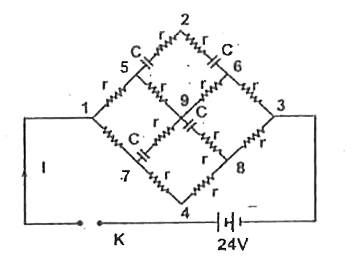
View SolutionFind charge on each capacitor.
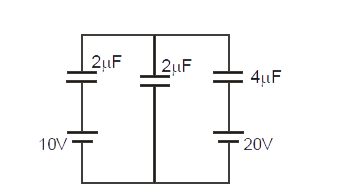
View SolutionFind charge on each capacitor.
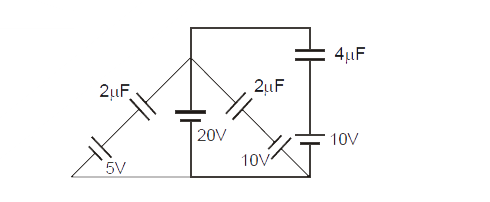
View SolutionFind charges on each capacitor.
MOT_CON_JEE_PHY_C25_SLV_009_Q01.png" width="80%">
View SolutionIn the circuit shown in the figure, find charge on each capacitor.

View SolutionIf A is connerted with D and B is connected with C find the potential difference a across each capacitor and the final charge in each capacitor.
View SolutionFind the final charge on each capacitor if they are connected as shown in the figure.

View Solution