A 6μF capacitor charged from 10 volts to 20 volts. Increase in energy will be -
18×10−4 Joule
9×10−4 Joule
4.5×10−4 Joule
9×10−9 Joule
The correct Answer is:B
To find the increase in energy of a capacitor when it is charged from 10 volts to 20 volts, we can follow these steps:
Step 1: Understand the Formula for Energy Stored in a Capacitor
The energy (U) stored in a capacitor is given by the formula:
U=12CV2
where:
- U is the energy in joules,
- C is the capacitance in farads,
- V is the voltage in volts.
Step 2: Calculate the Initial Energy at 10 Volts
Given:
- Capacitance C=6μF=6×10−6F
- Initial Voltage V1=10V
Using the formula:
U1=12CV21=12×(6×10−6)×(102)
Calculating:
U1=12×(6×10−6)×100=3×10−4 joules
Step 3: Calculate the Final Energy at 20 Volts
Given:
- Final Voltage V2=20V
Using the formula:
U2=12CV22=12×(6×10−6)×(202)
Calculating:
U2=12×(6×10−6)×400=12×10−4 joules=1.2×10−3 joules
Step 4: Calculate the Increase in Energy
The increase in energy (ΔU) is given by:
ΔU=U2−U1
Substituting the values:
ΔU=(1.2×10−3)−(3×10−4)
Calculating:
ΔU=1.2×10−3−0.3×10−3=0.9×10−3 joules=9×10−4 joules
Final Answer
The increase in energy when the capacitor is charged from 10 volts to 20 volts is:
ΔU=9×10−4 joules
---
The energy (U) stored in a capacitor is given by the formula:
U=12CV2
where:
- U is the energy in joules,
- C is the capacitance in farads,
- V is the voltage in volts.
Given:
- Capacitance C=6μF=6×10−6F
- Initial Voltage V1=10V
U1=12CV21=12×(6×10−6)×(102)
Calculating:
U1=12×(6×10−6)×100=3×10−4 joules
Given:
- Final Voltage V2=20V
U2=12CV22=12×(6×10−6)×(202)
Calculating:
U2=12×(6×10−6)×400=12×10−4 joules=1.2×10−3 joules
The increase in energy (ΔU) is given by:
ΔU=U2−U1
Substituting the values:
ΔU=(1.2×10−3)−(3×10−4)
Calculating:
ΔU=1.2×10−3−0.3×10−3=0.9×10−3 joules=9×10−4 joules
The increase in energy when the capacitor is charged from 10 volts to 20 volts is:
ΔU=9×10−4 joules
Topper's Solved these Questions
Similar Questions
A10μF capacitor is charged to 200 V and is isolated. It is then connected to another 10μF uncharged capacitor. The total electrostatic energy of the capacitor remains conserved.
View SolutionThe charge on a 48 μF capacitor is increased from 0.1 C to 0.5 C. the enerrgy stored in the capacitor increases by
View Solution
Knowledge Check
- Question 1 - Select One
If the potential of a capacitor having capacity of 6μF is increased from 10 V to 20 V,then increase in its energy will be
A12×10−6JB9×10−4JC4×10−6JD4×10−9J - Question 2 - Select One
A 16μF capacitor is charged to 20 volts. The battery is then disconnected and a pure 40mH coil is connected across the capacitor so that LC oscillations are set up. The maximum current in the coil is
A0.2AB40mAC2AD0.4A - Question 3 - Select One
A capacitor of capacitance 50μF is charged to 100 volts. Its energy is equal to
A25×10−2JB25×10−3JC25×10−4JD25×10−6J
A capacitor of 10μF charged up to 250 volts is connected in parallel with another capacitor of 5μF charged up to 100 volts. The common potential is
View SolutionA capacitor of 30μF charged up to 500 volt is connected in parallel with another capacitor of 15μF which is charged up to 300V. The common potential is
View SolutionA capacitorn of 2μF charged to 50 V is connected in parallel with another capacitor of 1μF charged to 20 V. The common potential and loss of energy will be
View SolutionA 2μF capacitor is charged with 10 volt cell. Now cell is removed and this capacitor is connected with uncharged 8μF capacitor. Find out final charge on 8μF capacitor.
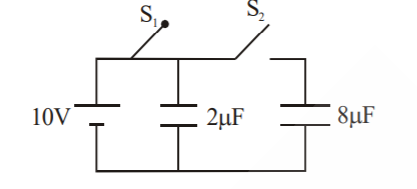 View Solution
View SolutionA capacitor of 20μF is charged to 500 volts and connected in parallel ith another capacitor of 10μF and charged to 200 volts. The common potential is
View Solution

