An air capacitor, a capacitor with a dielectric and a capacitor with a conducting slab (thickness one half the separation introducing between the plates of parallel plate air capacitor in both case) has capacity C1,C2andC3 respectively then :
C1>C2>C3
C2>C3>C1
C3>C2>C1
C3>C1>C2
The correct Answer is:B
To solve the problem of comparing the capacitance of three types of capacitors: an air capacitor (C1), a capacitor with a dielectric slab (C2), and a capacitor with a conducting slab (C3), we will derive the expressions for each capacitance and then compare them.
Step 1: Capacitance of the Air Capacitor (C1)
The formula for the capacitance of a parallel plate capacitor filled with air (or vacuum) is given by:
C1=ε0Ad
Where:
- ε0 is the permittivity of free space,
- A is the area of the plates,
- d is the separation between the plates.
Step 2: Capacitance of the Capacitor with a Dielectric Slab (C2)
When a dielectric slab of thickness d2 is inserted between the plates, the capacitor can be treated as two capacitors in series: one with the dielectric and one with air.
1. The capacitance of the portion with the dielectric slab is:
Cdielectric=kε0Ad2=2kε0Ad
2. The capacitance of the portion with air (the remaining d2) is:
Cair=ε0Ad2=2ε0Ad
3. The total capacitance C2 of the system is given by the formula for capacitors in series:
1C2=1Cdielectric+1Cair
Substituting the values we calculated:
1C2=d2kε0A+d2ε0A
Finding a common denominator:
1C2=d2ε0A(1k+1)
Thus,
C2=2ε0Ad(1k+1)=2kε0Ad(k+1)
Step 3: Capacitance of the Capacitor with a Conducting Slab (C3)
When a conducting slab of thickness d2 is placed between the plates, the electric field inside the conductor is zero. The effective distance between the plates is reduced to d−d2=d2.
Thus, the capacitance C3 is given by:
C3=ε0Ad2=2ε0Ad
Step 4: Comparing the Capacitances
Now we have:
- C1=ε0Ad
- C2=2kε0Ad(k+1)
- C3=2ε0Ad
Since k>1, we can deduce that:
1. C2>C3 because 2kk+1>2.
2. C3>C1 because 2ε0Ad>ε0Ad.
Thus, the order of capacitance is:
C2>C3>C1
Final Answer:
The capacitance values can be compared as follows:
C2>C3>C1
- ε0 is the permittivity of free space,
- A is the area of the plates,
- d is the separation between the plates.
- C1=ε0Ad
- C2=2kε0Ad(k+1)
- C3=2ε0Ad
2. C3>C1 because 2ε0Ad>ε0Ad.
The capacitance values can be compared as follows:
C2>C3>C1
Topper's Solved these Questions
Similar Questions
A metal slab of thickness, equal to half the distance between the plates is introduced between the plates of a parallel plate capacitor as shown. Find its capacity.
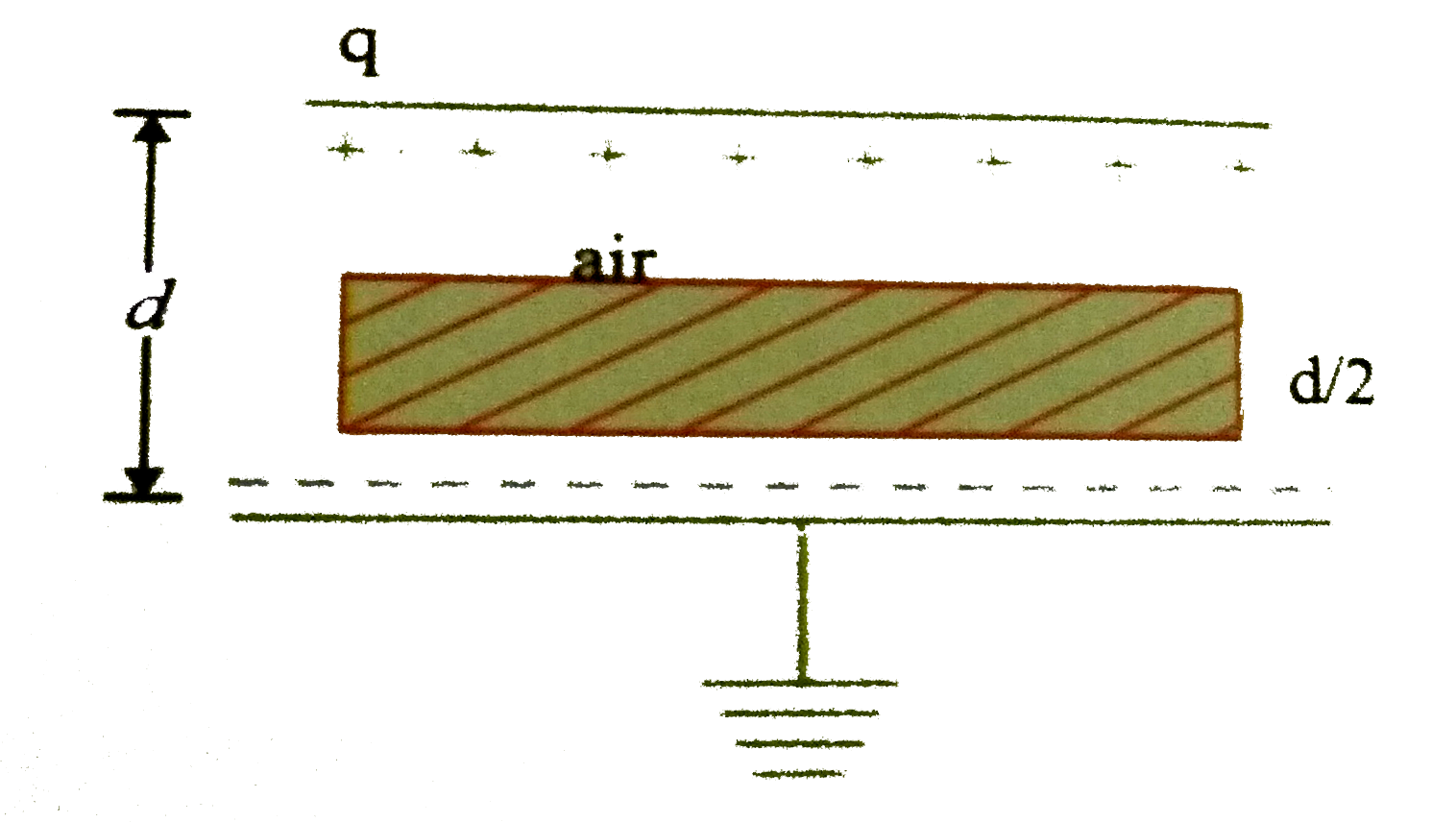 .
.
View SolutionA conducting slab of thickness 't' is introduced without touching between the plates of a parallel plate capacitor , separated by a distance 'd' (t<d) . Derive an expression for the capacitance of the capacitor .
View Solution
Knowledge Check
A dielectric slab is placed between the plates of a parallel plate capacitor. Its capacitance
Abecomes zeroBremains the sameCdecreasesDincreasesIf a dielectric slab of thickness 5 mm and dielectric constant K=6 is introduced between the plates of a parallel plate air capacitor, with plate separation of 8 mm, then its capacitance is
A1. decreasedB2. unaffectedC3. almost halvedD4. almost doubledA metal plate of thickness half the separation between the capacitor plates of capacitance C is inserted. The new capacitance is.
ACBC/2CzeroD2C
What is a parallel plate capacitor? Obtain an expression for the capacitance of a parallel plate capacitor when a conducting slab is inserted between its plates.
View SolutionA parallel -plate air capacitor has capacity C. A dielectric slab of dielectric constant K, whose thickness is half of the air gap between the plates, is now inserted between the plates. The capacity of the capacitor will now be
View SolutionA metallic plate of thickness (t) and face area of one side (A) is inserted between the plates of a parallel plate air capacitor with a separation (d) and face are (A). Then the equivalent capacitance is
View Solutionparallel plate capacitor has capacitance C when no dielectric between thw plates. Now a slab of dielectric constant K, having same thickness as the separation between the plates is introduced so as to fill one-fourth of the capacitor as shown in the figure. the new capacitance will be
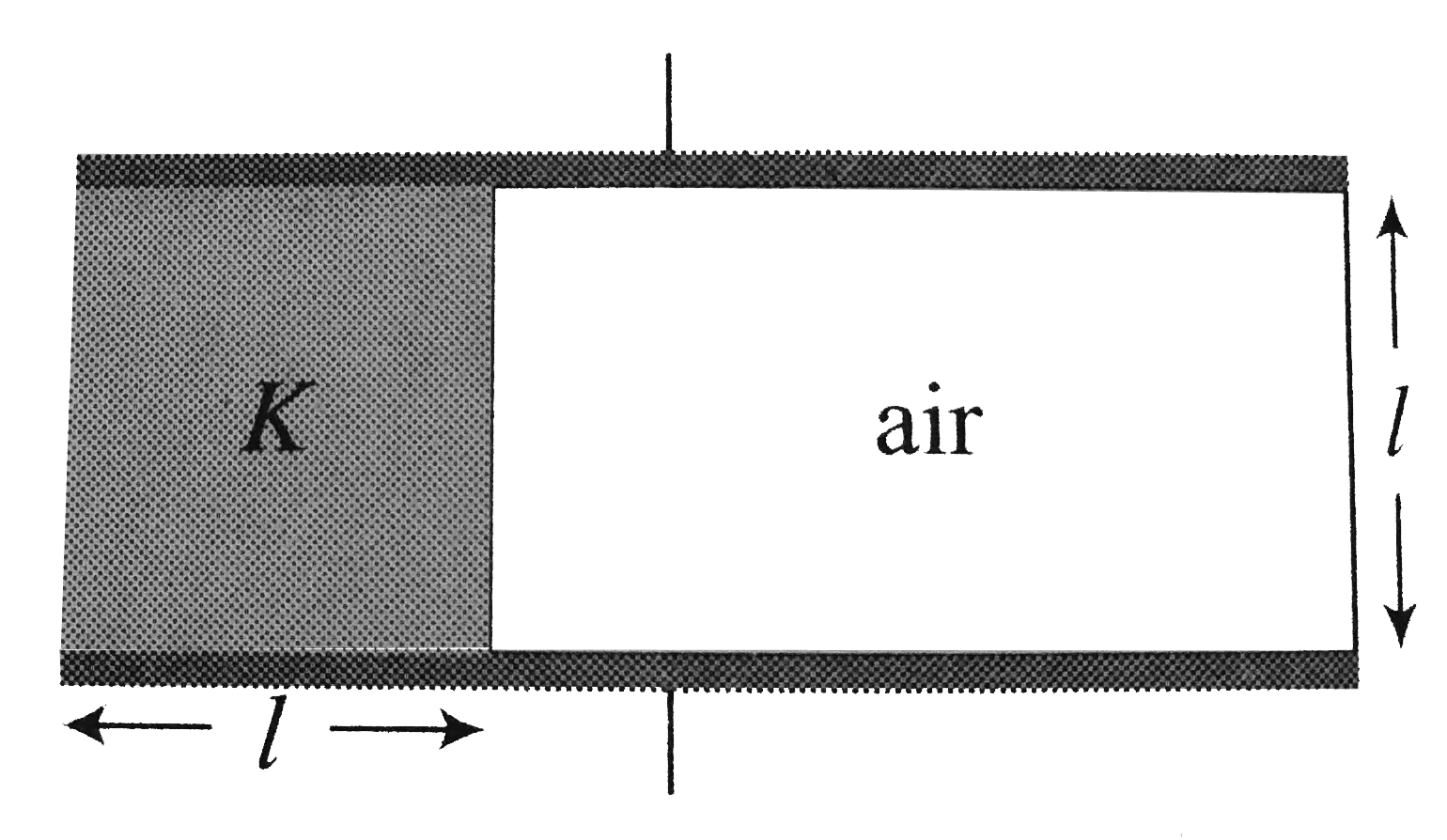
View SolutionA parallel plate air capacitor has capacity C distance of separation between plates is d and potential difference V is applied between the plates force of attraction between the plates of the parallel plate air capacitor is
View Solution
