Question

Write a pair of linear equations which has the unique solution $x=-1$ and $y=3$. How many such pairs can you write ?

Explanation

Condition for the pair of system to have unique solution
`(a_(1))/(a_(2))!=(b_(1))/(b_(2))`
Let the equations are,
`a_(1)x+b_(1)y+c_(1)=0`
and `" " a_(2)x+b_(2)y+c_(2)=0`
Since, x=-1 and y=3 is the unique solution of these two equations, then
`a_(1)(-1)+b_(1)(3)+c_(1)=0`
`rArr " " -a_(1)+3b_(1)+c_(1)=0 " " ...(i)`
and `" " a_(2)(-1)+b_(2)(3)+c_(2)=0 `
`rArr " " -a_(2)+3b_(2)+c_(2)=0 " " ...(ii)`
So, the different values of `a_(1), a_(2), b_(1), b_(2), c_(1)` and `c_(2)` satisfy the Eqs. (i) and (ii).

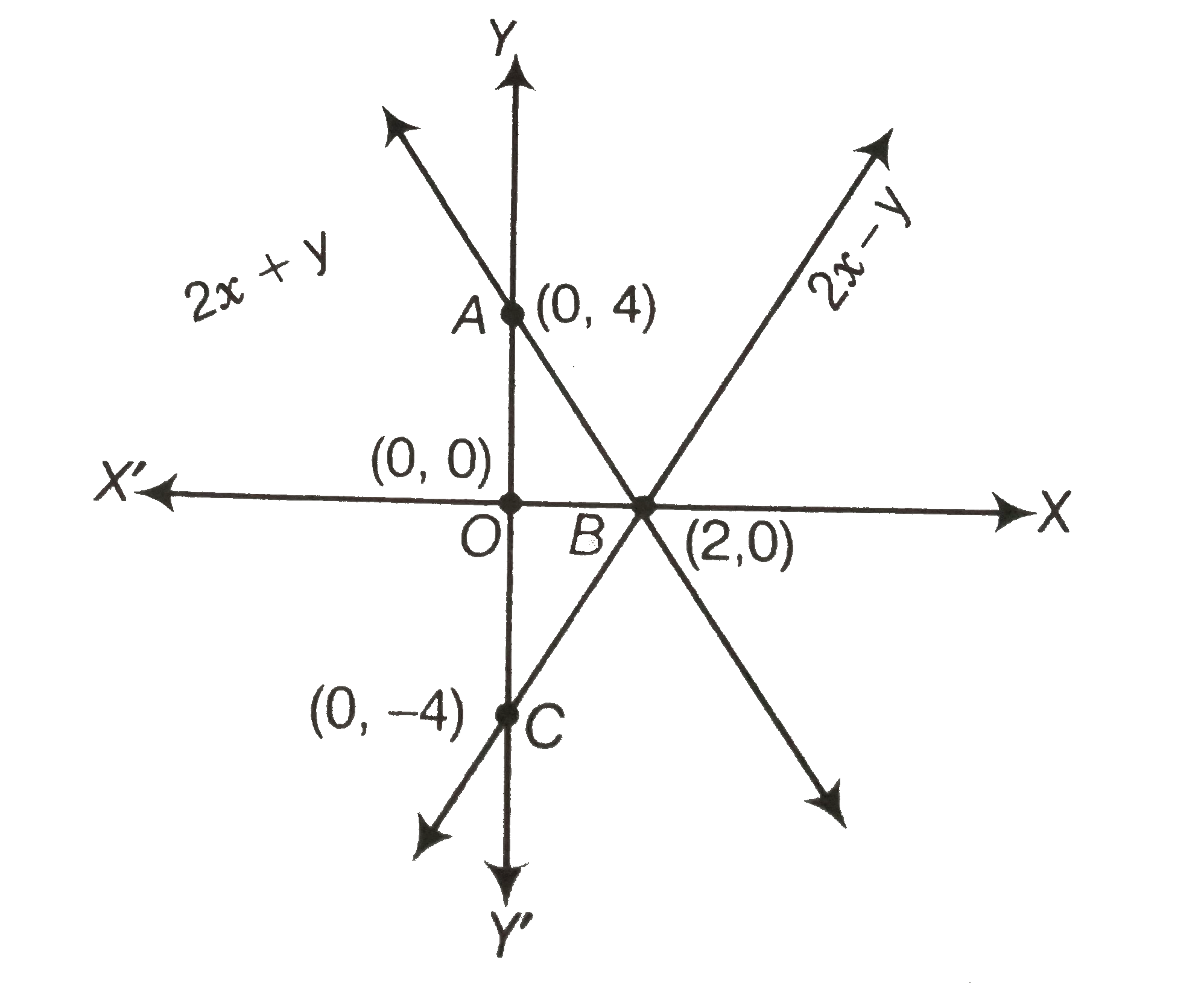
Hence, infinitely many pairs of linear equations are possible.