The maximum distance of a point on the graph of the function $y = \sqrt{3} sin x + cos x$ from X-axis is

Video Solution

Text Solution

Verified by Experts

Given that, $y = \sqrt{3} sin x + cos x$
$y = 2 [\frac{\sqrt{3}}{2} sin x + \frac{1}{2} cos x]$
$= 2 [sin x \cdot cos \frac{π}{6} + cos x sin \frac{π}{6}]$
$= 2 sin (x + π / 6)$
Graph of y = $2 sin x$

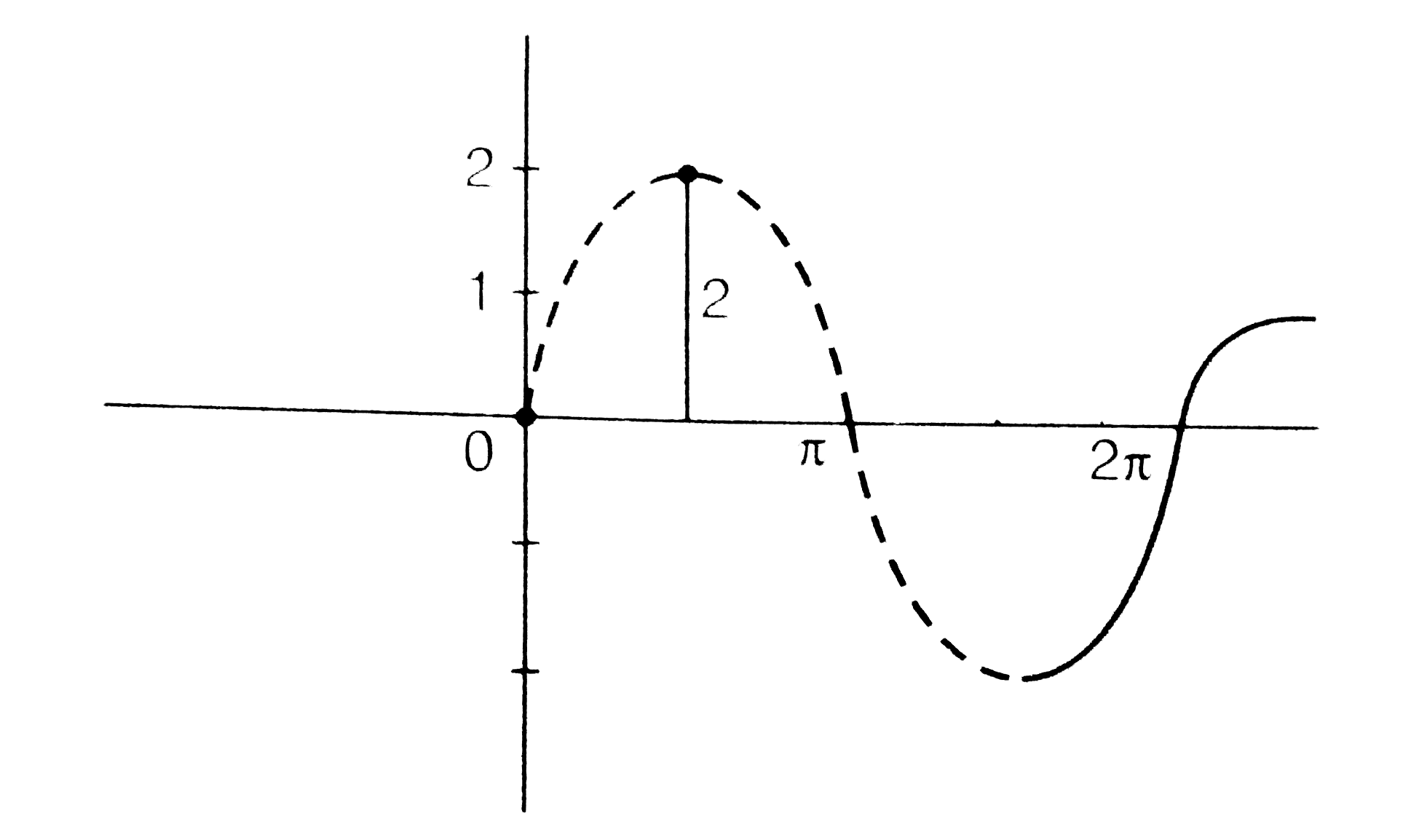
Hence, the maximum distance is 2 units.

Updated on:21/07/2023

|

Class 11 MATHS TRIGONOMETRIC FUNCTIONS

Topper's Solved these Questions

TRIGONOMETRIC FUNCTIONS BOOK - NCERT EXEMPLARCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - TRUE/FALSE
9 Videos
TRIGONOMETRIC FUNCTIONS BOOK - NCERT EXEMPLARCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - OBJECTIVE TYPE QUESTIONS
31 Videos
STRAIGHT LINESBOOK - NCERT EXEMPLARCHAPTER - STRAIGHT LINESEXERCISE - MATCHING THE COLUMN
3 Videos

Similar Questions

Knowledge Check

$\sqrt{3} sin x + cos x$ is maximum when x is
A $30^{\circ}$
B $90^{\circ}$
C $60^{\circ}$
D $45^{\circ}$

NCERT EXEMPLAR-TRIGONOMETRIC FUNCTIONS -FILLERS

Home
Ask Doubt
Profile