Using the digits 1, 2, 3, 4, 5, 6,7, a number of 4 different digits is formed. Find
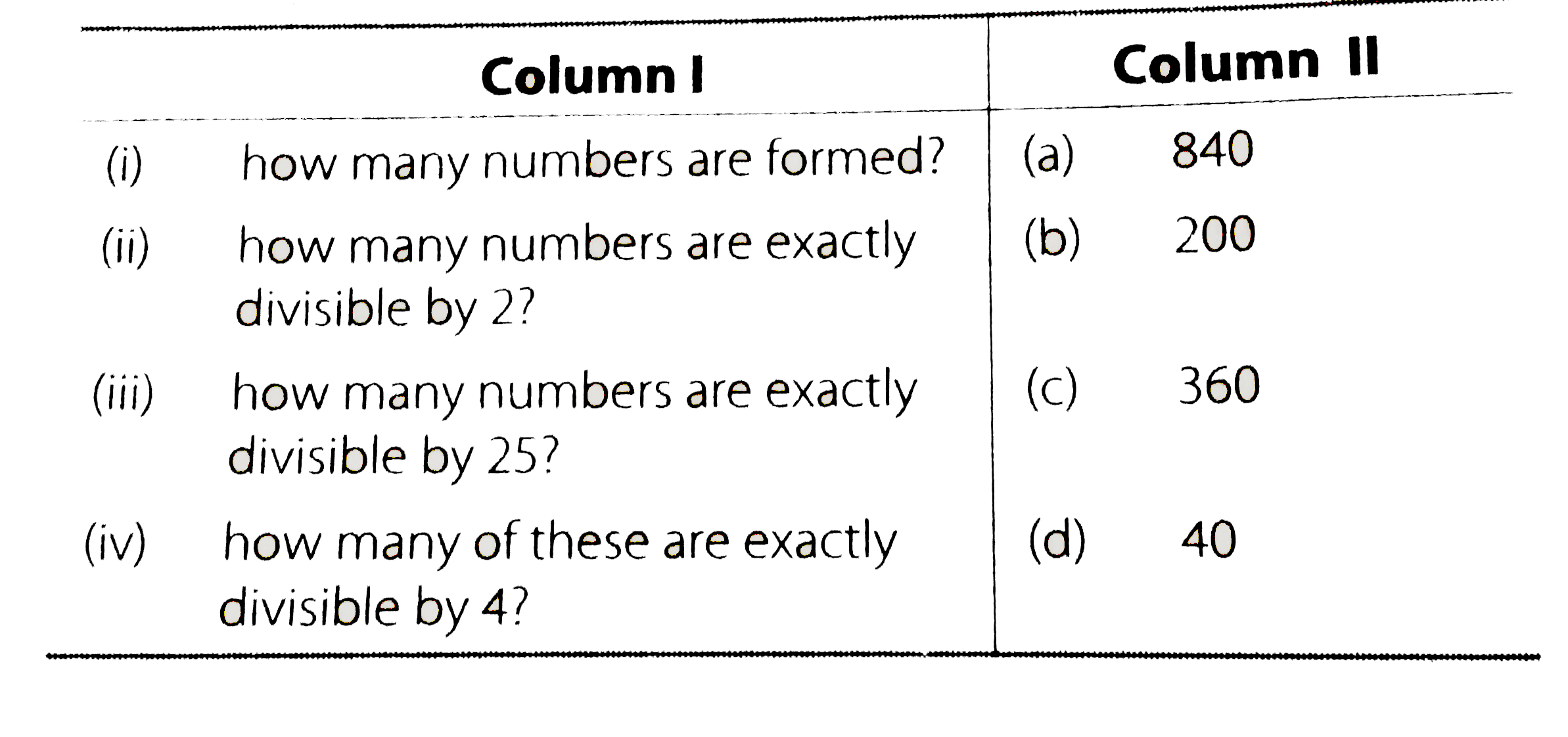
(i) Total number of 4 digit formed with digit 1, 2, 3, 4, 5, 6, 7
=7×6×5×4=840
(ii) When a number is divisible by 2. At its unit place only even numbers occurs.
Total numbers =4×5×6×3=360
(iii) Total numbers which are divisible by 25 = 40
(iv) A number is divisible 4, If its last two digit is divisible by 4.
∴ Total such numbers = 200
Topper's Solved these Questions
- PERMUTATIONS AND COMBINATIONSBOOK - NCERT EXEMPLARCHAPTER - PERMUTATIONS AND COMBINATIONSEXERCISE - True/False
9 Videos
- MATHEMATICAL REASONING BOOK - NCERT EXEMPLARCHAPTER - MATHEMATICAL REASONING EXERCISE - OBJECTIVE TYPE QUESTIONS
21 Videos
- PRINCIPLE OF MATHEMATICAL INDUCTION BOOK - NCERT EXEMPLARCHAPTER - PRINCIPLE OF MATHEMATICAL INDUCTION EXERCISE - OBJECTIVE TYPE QUESTIONS
5 Videos
Similar Questions
Four digit numbers with different digits are formed using the digits 1,2,3,4,5,6,7,8. One number from them is picked up at random. The chance that the selected number contains the digit '1' is
View SolutionA five digit number (having all different digits) is formed using the digits 1,2,3,4,5,6,7,8and9. The probability that the formed number either begins or ends with an odd digit, is equal to
View Solution
Knowledge Check
The number of five-digit numbers which are divisible by 3 that can be formed by using the digits 1,2,3,4,5,6,7,8 and 9, when repetition of digits is allowed, is
A39B4.38C5.38D7.38A four digit number of distinct digits is formed by using the digits 2, 3, 4, 5, 6, 7, 8. The number of such numbers which are divisible by 25, is
A60B40C20D15How many even numbers of 3 different digits can be formed from the digits 1, 2, 3, 4, 5, 6, 7, 8, 9 (repetition of digits is not allowed) ?
A224B280C324DNone of these
How many four-digit numbers can be formed by using the digits 1, 2, 3, 4, 5, 6, 7 if at least one digit is repeated.
View SolutionThe number of four-digit numbers that can be formed by using the digits 1,2,3,4,5,6,7,8 and 9 such that the least digit used is 4, when repetition of digits is allowed is
View SolutionFind the number of 6-digit numbers that can be found using the digits 1, 2, 3, 4, 5, 6 once such that the 6-digit number is divisible by its unit digit. (The unit digit is not 1).
View SolutionA number of 4 different digits is formed by using the digits 1, 2, 3, 4, 5, 6, 7 in all possible ways without repetition. How many of them are exactly divisible by 4?
View SolutionA number of 4 different digits is formed by using the digits 1, 2, 3, 4, 5, 6, 7 in all possible ways without repetition.
How many of them are greater than 3400?
View Solution
