S1 and S2 are two loudspeakers with the same frequency of 165 Hz and acoustic output 1.2×10−3 and 1.8×10−3 watts respectively/ They vibrate in the same phase. P is a point at a distance 4m from S1 and 3m from S2
What is the intensity at P with S1 and S2 on?
The correct Answer is:A, C
Topper's Solved these Questions
- WAVES BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WAVES EXERCISE - Advance MCQs with One or More Options Correct
30 Videos
- WAVE OPTICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WAVE OPTICSEXERCISE - Unsolved Numerical Problems
28 Videos
- X-RAYSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - X-RAYSEXERCISE - Unsolved Numerica Problem for Preparation
23 Videos
Similar Questions
S1 and S2 are two loudspeakers with the same frequency of 165 Hz and acoustic output 1.2×10−3 and 1.8×10−3 watts respectively/ They vibrate in the same phase. P is a point at a distance 4m from S1 and 3m from S2
What is the intensity of sound at P if S2 is turned off?
View SolutionS1 and S2 are two loudspeakers with the same frequency of 165 Hz and acoustic output 1.2×10−3 and 1.8×10−3 watts respectively/ They vibrate in the same phase. P is a point at a distance 4m from S1 and 3m from S2
What is the intensity of sound at P if S1 is turned off (S2) on)
View Solution
Knowledge Check
Consider two coherent, monochromatic (wavelength λ) sources S1andS2, separated by a distance d. The ratio of intensities of S1 and that of S2 (which is responsible for interference at point P, where detector is located) is 4. The distance of point P from S1 is (if the resultant intensity at point P is equal to 94 times of intensity of S1) (Given : ∠S2S1P=90∘,d>0andn is a positive integer)
Ad2−n2λ22nλBd2+n2λ22nλCnλd√d2−n2λ2D2nλd√d2−n2λ2
S1 and S2 are two loudspeakers with the same frequency of 165 Hz and acoustic output 1.2×10−3 and 1.8×10−3 watts respectively/ They vibrate in the same phase. P is a point at a distance 4m from S1 and 3m from S2
How are the phase of the two waves arriving at P related?
View SolutionS1 and S2 are two loudspeakers with the same frequency of 165 Hz and acoustic output 1.2×10−3 and 1.8×10−3 watt respectively. They vibrate in the same phase. P is a point at a distance 4 m from S1 and 3 m from S2.
(a) How are the phases of the two waves arriving at P related ?
(b) What is the intensity of P if S1 is turned off (S2 on)?
(c) What is the intensity of sound at P if S2 is turmed off ?
(d) What is the intensity at P with S1 and S2 on ?
[Hint : For phase relationship see example 6 of chapter 1. Intensity is inversely proportional to square of the distance]
View SolutionTwo loudspeakers S1 and S2 each emit sounds of frequency 220HZ uniformly in all directions. S1 has an acoustic output of 1.2×10−3W and S2 has 1.8×10−3W . S1 and S2 vibrate in phase.Consider a point P such that S1P=0.75m and S2p=3m . How are the phases arriving at P related? What is the intensity at P when both S1 and S2 are on ? Speed of sound in air is 330m/s.
View SolutionTwo loudspeakers S1 and S2 each emit sounds of frequency 220HZ uniformly in all directions. S1 has an acoustic output of 1.2×10−3W and S2 has 1.8×10−3W . S1 and S2 vibrate in phase.Consider a point P such that S1P=0.75m and S2p=3m . How are the phases arriving at P related? What is the intensity at P when both S1 and S2 are on ? Speed of sound in air is 330m/s.
View SolutionConsider two coherent, monochromatic (wavelength λ) sources S1andS2, separated by a distance d. The ratio of intensities of S1 and that of S2 (which is responsible for interference at point P, where detector is located) is 4. The distance of point P from S1 is (if the resultant intensity at point P is equal to 94 times of intensity of S1) (Given : ∠S2S1P=90∘,d>0andn is a positive integer)
View SolutionS1 and S2 are two equally intense coherent point second sources vibrating in phase. The resultant intensity at P1 is 80SI units then resultant intensity at P2 in SI units will be
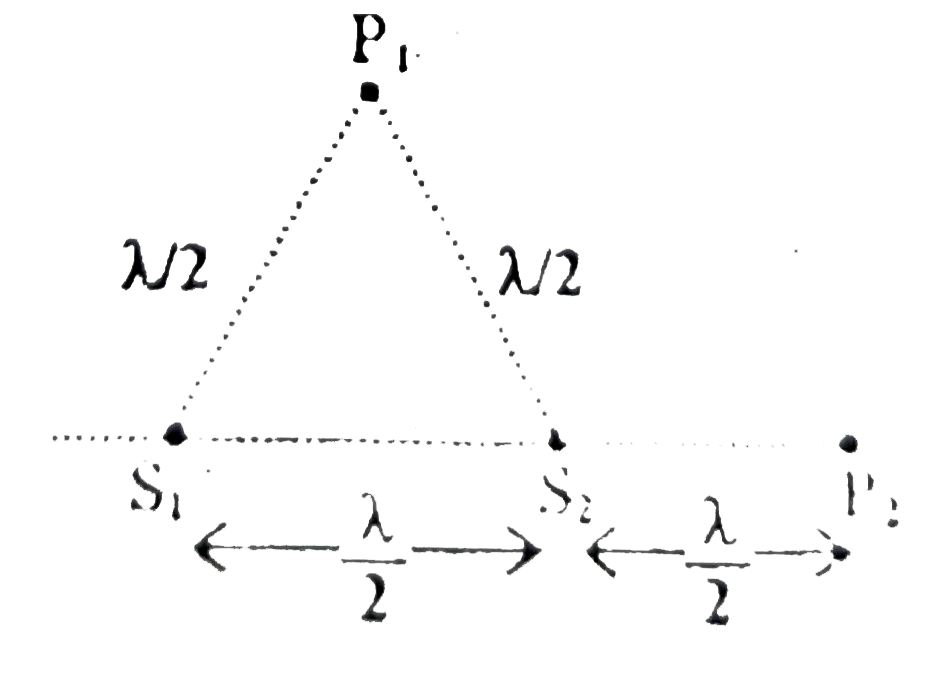
View SolutionS1 and S2 are two equally intense coherent point second sources vibrating in phase. The resultant intensity at P1 is 80SI units then resultant intensity at P2 in SI units will be

View Solution
