Compute the area of the figure bounded by the straight lines x=0,x=2 and the curvesy=2x,y=2x−x2
Video Solution
Text Solution
We have to find the area of the region bounded by
the
straight lines x=0,x=2
and
the curvesy=2x,y=2x−x2
so area is,
A=∫20(2x−2x+x2)dx
=[2xln(2)+(x−3)x23]20
=[4ln2−43]−[1ln2]
=3log2−43
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
The area of the figure bounded by the curves y2=2x+1 and x−y−1=0 , is
A2/3B4/3C8/3D16/3
The area of the region bounded by the straight lines y=x,y=2x and y=2 ,is
View SolutionThe area of the region bounded by the straight lines y=x,y=2x and y=2 ,is
View SolutionCompute the area of the figure bounded by the parabolas x=−2y2,x=1−3y2
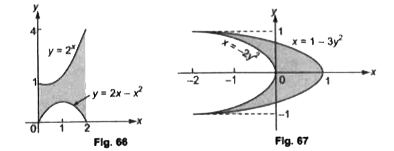 View Solution
View SolutionFind the area of the figure bounded by the curve y=sin−1x, the lines x=0 and y=π2.
View SolutionCompute the area of the figure bounded by the curve √x+√y=1 and the straight line x+y=1
View SolutionFind the area of the region bounded by the curves y=x2+2, y=x,x=0andx=3.
View SolutionThe area of the region bounded by the curve y=2x−x2 and the line y=x is
View Solution

