A body is projected at an angle θ with the horizontal. Derive an expression for its horizontal range. Show that there are two angles θ1 and θ2 projections for the same horizontal range, such that θ1+θ2=90∘.
To derive the expression for the horizontal range of a projectile launched at an angle θ with the horizontal, we can follow these steps:
Step 1: Resolve the Initial Velocity
The initial velocity u of the projectile can be resolved into two components:
- Horizontal component: ux=ucosθ
- Vertical component: uy=usinθ
Step 2: Determine the Time of Flight
The time of flight T can be calculated by analyzing the vertical motion. The projectile will rise to its highest point and then fall back down. The time to reach the highest point is given by:
t=uyg=usinθg
Since the time to go up is equal to the time to come down, the total time of flight T is:
T=2t=2usinθg=2usinθg
Step 3: Calculate the Horizontal Range
The horizontal range R can be found using the horizontal motion. The horizontal distance traveled is given by:
R=ux⋅T=(ucosθ)⋅(2usinθg)
Substituting ux and T into the equation gives:
R=2u2sinθcosθg
Step 4: Use the Double Angle Identity
Using the double angle identity for sine, sin2θ=2sinθcosθ, we can simplify the expression for range:
R=u2sin2θg
Step 5: Show that there are Two Angles for the Same Range
To show that there are two angles θ1 and θ2 that give the same range, we can set the ranges equal:
R1=R2⟹u2sin2θ1g=u2sin2θ2g
This simplifies to:
sin2θ1=sin2θ2
From the properties of the sine function, we know:
2θ2=180∘−2θ1⟹θ1+θ2=90∘
Conclusion
Thus, we have derived the expression for the horizontal range R of a projectile and shown that there are two angles θ1 and θ2 such that θ1+θ2=90∘ that yield the same range.
---
The initial velocity u of the projectile can be resolved into two components:
- Horizontal component: ux=ucosθ
- Vertical component: uy=usinθ
The time of flight T can be calculated by analyzing the vertical motion. The projectile will rise to its highest point and then fall back down. The time to reach the highest point is given by:
t=uyg=usinθg
Since the time to go up is equal to the time to come down, the total time of flight T is:
T=2t=2usinθg=2usinθg
The horizontal range R can be found using the horizontal motion. The horizontal distance traveled is given by:
R=ux⋅T=(ucosθ)⋅(2usinθg)
Substituting ux and T into the equation gives:
R=2u2sinθcosθg
Using the double angle identity for sine, sin2θ=2sinθcosθ, we can simplify the expression for range:
R=u2sin2θg
To show that there are two angles θ1 and θ2 that give the same range, we can set the ranges equal:
R1=R2⟹u2sin2θ1g=u2sin2θ2g
This simplifies to:
sin2θ1=sin2θ2
From the properties of the sine function, we know:
2θ2=180∘−2θ1⟹θ1+θ2=90∘
Thus, we have derived the expression for the horizontal range R of a projectile and shown that there are two angles θ1 and θ2 such that θ1+θ2=90∘ that yield the same range.
Topper's Solved these Questions
- KINEMATICSBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - KINEMATICSEXERCISE - 5 Marks
2 Videos
- KINEMATICSBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - KINEMATICSEXERCISE - Numericals
26 Videos
- KINEMATICSBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - KINEMATICSEXERCISE - 2 Marks
14 Videos
- GRAVITATIONBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - GRAVITATIONEXERCISE - MULTIPLE CHOICE QUESTIONS
19 Videos
- KINETIC THEORY OF GASESBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - KINETIC THEORY OF GASESEXERCISE - Objective question
20 Videos
Similar Questions
Knowledge Check
If a body is projected with an angle θ to the horizontal, then
Aits velocity is always perpendicular to its accelerationBits velocity becomes zero at its maximum height.Cits velocity makse zero angle with the horizontal at its maximum heightDthe body just before hitting the ground, the direction of velocity coincides with the accelerationA particle is projected at an angle with horizontal. If T is the time of flight and R is a horizontal range, then θ is
Acot−1(gT2R)Bcot−1(gT22R)Ctan−1(2RgT2)Dtan−1(gT22R)A particle is projected at an angle θ=30∘ with the horizontal, with a velocity of 10ms−1. Then
AAfter 2 s, the velocity of particle makes an angle of 60∘ with initial velocity vector.BAfter 1 s, the velocity of particles makes an angle of 60∘ with initial velocity vector.CThe magnitude of velocity of particle after 1 s is 10ms−1.DThe magnitude of velocity of particle after 1 s is 5ms−1.
A body is projected with speed u at an angle θ to the horizontal to have maximum range. Its velocity at the highest point will be ___.
View Solution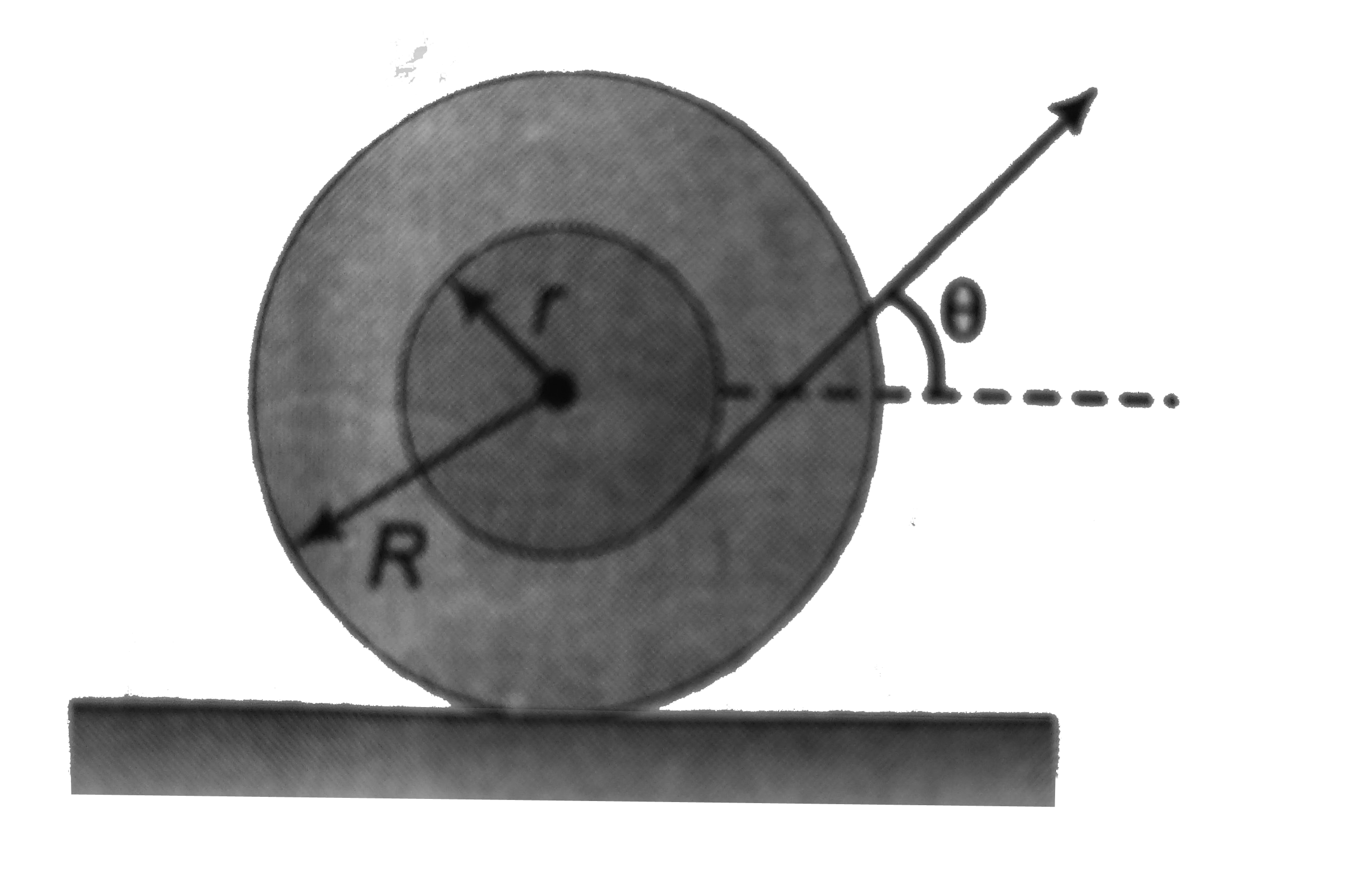
A spool is pulled at an angle θ with the horizontal on a rough horizontal surface as shown in the figure. If the spool remains at rest, the angle θ is equal to
View SolutionA ball is thrown at an angle θ with the horizontal and the range is maximum. The value of tanθ is:-
View SolutionA body of mass m is projected with intial speed u at an angle θ with the horizontal. The change in momentum of body after time t is :-
View SolutionA body projected at an angle θ to the horizontal with kinetic energy Ek . The potential energy at the highest point of the trajectory is
View Solution
