If the angle between the vectors →Aand→B is θ, the value of the product (→B×→A)⋅→A is equal to
A
BA2cosθ
B
BA2sinθ
C
BA2sinθcosθ
D
Zero
Video Solution
Text Solution
The correct Answer is:D
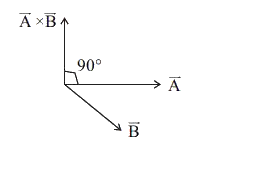
Angle between →B×→Aand→A is 90∘
(→B×→A).→A=∣∣→B×→A∣∣∣∣→A∣∣cos90∘
=0
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - KINEMATICSEXERCISE - Numericals26videos
KINEMATICS
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - GRAVITATIONEXERCISE - MULTIPLE CHOICE QUESTIONS19videos
GRAVITATION
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - KINETIC THEORY OF GASESEXERCISE - Objective question20videos
KINETIC THEORY OF GASES
Similar Questions
Knowledge Check
- Question 1 - Select One
The angle between the vector →A and →B is θ. The value of the triple product →A.(→B×→A) is
AA2BBZeroCA2BsinθDA2cosθ - Question 2 - Select One
The angle between vectors (→A×→B)and(→B×→A) is :
Aπ radBπ2 radCπ4 radDzero - Question 3 - Select One
If →a,→band→c are three vectors, such that |→a|=2,∣∣→b∣∣=3,|→c|=4,→a.→c=0,→a.→b=0 and the angle between →band→c is π3, then the value of ∣∣→a×(2→b−3→c)∣∣ is equal to
A12√3B6√3C3√3D5
If the vectors →a and →b are mutually perpendicular, then →a×{→a×{→a×{→a×→b}} is equal to:
View SolutionIf θ is the angle between unit vectors →A and →B, then (1−→A.→B)1+→A.→B⎞⎟ ⎟⎠ is equal to
View SolutionThe value of the sum of two vectors →A and →B with θ as the angle between them is
View SolutionAssertion: If θ be the angle between →A and →B then tanθ=→A×→B→A.→B
Reason: →A×→B is perpendicular to →A.→BView SolutionIf →a,→band→c are non- coplanar vectors and →a×→c is perpendicular to →a×(→b×→c) , then the value of [→a×(→b×→c)]×→c is equal to
View Solution


