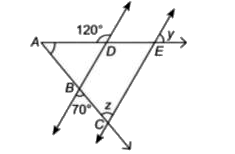
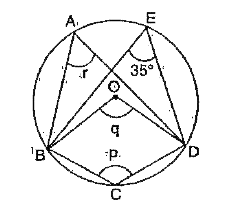
In the figure , If AB||CE, then find the values of p , q and r.
The correct Answer is:33∘,57∘,65∘
To find the values of p, q, and r given that AB∥CE, we can follow these steps:
1. Identify the Given Information:
- We know that AB∥CE.
- AC acts as a transversal line intersecting the parallel lines.
2. Use Alternate Angles:
- Since AB∥CE and AC is a transversal, we can use the property of alternate interior angles.
- Therefore, q=32∘ (as given in the problem).
Hint: Recall that alternate interior angles are equal when two lines are parallel and cut by a transversal.
3. Apply the Triangle Angle Sum Property:
- In triangle ABC, the sum of the angles is 180∘.
- We know one angle is 90∘ (let's assume ∠ABC=90∘) and q=32∘.
- Therefore, we can write the equation:
p+90∘+q=180∘
Substituting q:
p+90∘+32∘=180∘
Hint: Remember that the sum of angles in a triangle is always 180∘.
4. Solve for p:
- Rearranging the equation gives:
p+122∘=180∘
p=180∘−122∘=58∘
Hint: Isolate p by subtracting the known angle sum from 180∘.
5. Determine r:
- The angle r is an exterior angle to triangle ACE.
- The exterior angle theorem states that the exterior angle is equal to the sum of the two opposite interior angles.
- Therefore:
r=θ+q
Since θ=p=58∘ and q=32∘:
r=58∘+32∘=90∘
Hint: Recall that the exterior angle is equal to the sum of the two non-adjacent interior angles.
Final Values:
- p=58∘
- q=32∘
- r=90∘
- We know that AB∥CE.
- AC acts as a transversal line intersecting the parallel lines.
- Since AB∥CE and AC is a transversal, we can use the property of alternate interior angles.
- Therefore, q=32∘ (as given in the problem).
- In triangle ABC, the sum of the angles is 180∘.
- We know one angle is 90∘ (let's assume ∠ABC=90∘) and q=32∘.
- Therefore, we can write the equation:
p+90∘+q=180∘
Substituting q:
p+90∘+32∘=180∘
- Rearranging the equation gives:
p+122∘=180∘
p=180∘−122∘=58∘
- The angle r is an exterior angle to triangle ACE.
- The exterior angle theorem states that the exterior angle is equal to the sum of the two opposite interior angles.
- Therefore:
r=θ+q
Since θ=p=58∘ and q=32∘:
r=58∘+32∘=90∘
- p=58∘
- q=32∘
- r=90∘
Topper's Solved these Questions
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - LINES AND ANGLESEXERCISE - PART-C16videos
LINES AND ANGLES
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - LINES AND ANGLESEXERCISE - PART-D8videos
LINES AND ANGLES
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - LINES AND ANGLESEXERCISE - PRACTICE TEST8videos
LINES AND ANGLES
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - LINEAR EQUATIONS IN TWO VARIABLES EXERCISE - PRACTICE TEST12videos
LINEAR EQUATIONS IN TWO VARIABLES
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - NUMBER SYSTEMSEXERCISE - Part - D18videos
NUMBER SYSTEMS
Similar Questions
Knowledge Check
- Question 1 - Select One
In the given figure AB∣∣CE and BC∣∣FG. Find the value of x∘:
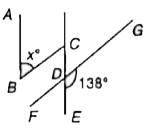 A52∘B32∘C42∘D36∘
A52∘B32∘C42∘D36∘ - Question 2 - Select One
If p, q and rare three statements and truth value of p∧q→ r is F, then truth values of p,q and r are respectively
AT, F, TBT, T ,FCF, T, TDF, F, T
In the given figure AB||CE and BC||FG, then value of x is.
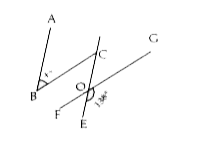 View Solution
View SolutionIn the figure, find the value of AB.
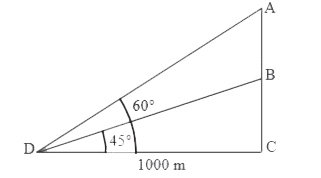 View Solution
View SolutionIf a and b vary inversely to each other, then find the values of p, q, r .
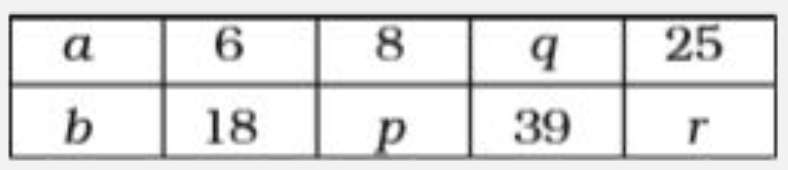 View Solution
View SolutionIn Fig. 6.43, if PQ⊥PS,PQ∣∣SR,∠SQR=28∘ and ∠QRT=65∘, then find the values of x and y.
 View Solution
View SolutionIn the figure ΔABC,DE∣∣AB. If AD=2x,DC=x+3,BE=2x−1CE=x then find the value of x.
 View Solution
View SolutionIf p=4 , q=-3, r=2 find the value of 4p2+5q−12r
View Solution