If the sum of the first four terms of an AP is 40 and the sum of the first fourteen terms of an AP is 280. Find the sum of first n terms of the A.P.
The correct Answer is:S4=40
S14=280 Solve to get a=7, d=2
To solve the problem, we need to find the sum of the first n terms of an arithmetic progression (AP) given the sums of the first 4 and 14 terms. Let's break down the solution step by step.
Step 1: Understand the formula for the sum of the first n terms of an AP
The formula for the sum of the first n terms of an AP is given by:
Sn=n2×(2a+(n−1)d)
where:
- Sn is the sum of the first n terms,
- a is the first term,
- d is the common difference,
- n is the number of terms.
Step 2: Write the equations based on the given information
We are given:
1. The sum of the first 4 terms (S4) is 40:
S4=42×(2a+(4−1)d)=40
Simplifying this, we get:
2×(2a+3d)=40⟹2a+3d=20(Equation 1)
2. The sum of the first 14 terms (S14) is 280:
S14=142×(2a+(14−1)d)=280
Simplifying this, we get:
7×(2a+13d)=280⟹2a+13d=40(Equation 2)
Step 3: Solve the system of equations
Now we have two equations:
1. 2a+3d=20 (Equation 1)
2. 2a+13d=40 (Equation 2)
We can subtract Equation 1 from Equation 2:
(2a+13d)−(2a+3d)=40−20
This simplifies to:
10d=20⟹d=2
Step 4: Substitute d back to find a
Now that we have d=2, we can substitute this value back into Equation 1 to find a:
2a+3(2)=20⟹2a+6=20⟹2a=14⟹a=7
Step 5: Find the sum of the first n terms
Now that we have a=7 and d=2, we can find the sum of the first n terms:
Sn=n2×(2a+(n−1)d)
Substituting the values of a and d:
Sn=n2×(2×7+(n−1)×2)
Sn=n2×(14+2n−2)=n2×(2n+12)
Sn=n×(n+6)
Final Result
Thus, the sum of the first n terms of the AP is:
Sn=n2+6n
The formula for the sum of the first n terms of an AP is given by:
Sn=n2×(2a+(n−1)d)
where:
- Sn is the sum of the first n terms,
- a is the first term,
- d is the common difference,
- n is the number of terms.
We are given:
1. The sum of the first 4 terms (S4) is 40:
S4=42×(2a+(4−1)d)=40
Simplifying this, we get:
2×(2a+3d)=40⟹2a+3d=20(Equation 1)
S14=142×(2a+(14−1)d)=280
Simplifying this, we get:
7×(2a+13d)=280⟹2a+13d=40(Equation 2)
Now we have two equations:
1. 2a+3d=20 (Equation 1)
2. 2a+13d=40 (Equation 2)
(2a+13d)−(2a+3d)=40−20
This simplifies to:
10d=20⟹d=2
Now that we have d=2, we can substitute this value back into Equation 1 to find a:
2a+3(2)=20⟹2a+6=20⟹2a=14⟹a=7
Now that we have a=7 and d=2, we can find the sum of the first n terms:
Sn=n2×(2a+(n−1)d)
Substituting the values of a and d:
Sn=n2×(2×7+(n−1)×2)
Sn=n2×(14+2n−2)=n2×(2n+12)
Sn=n×(n+6)
Thus, the sum of the first n terms of the AP is:
Sn=n2+6n
Topper's Solved these Questions
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ARITHMETIC PROGRESSION EXERCISE - PRACTICE TEST (SECTION A)4videos
ARITHMETIC PROGRESSION
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ARITHMETIC PROGRESSION EXERCISE - PRACTICE TEST (SECTION B)3videos
ARITHMETIC PROGRESSION
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ARITHMETIC PROGRESSION EXERCISE - SHORT ANSWER TYPE QUESTIONS-II17videos
ARITHMETIC PROGRESSION
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - AREAS RELATED TO CIRCLESEXERCISE - PRACTICE-TEST ( AREAS RELATED TO CIRCLES ) SECTION-D1videos
AREAS RELATED TO CIRCLES
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - CIRCLESEXERCISE - PRACTICE - TEST (SECTION - D)1videos
CIRCLES
Similar Questions
The sum of first 10 natural numbers.
03:35View SolutionHow many 2 digit number are ther in between 6 and 102 which are divisible by 6.
03:59View SolutionFind the middle term(s) of the A.P. 7, 13, 19, .., 241 .
03:16View SolutionA chord AB of a circle of radius 10 cm makes a right angle at the centre of the circle. Find the area of the major and minor segment. (Use π=3.14)
03:54View SolutionAB is a diameter of a circle with centre O and AT is a tangent. If ∠AOQ=58∘ find ∠ATQ.
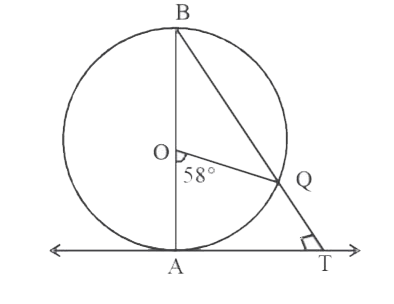 03:14View Solution
03:14View SolutionIf the sum of first 7 terms of an AP is 49 and that of 17 terms is 289, find the sum of first n terms.
03:26View SolutionThe sum of the first five terms of an AP and the sum of the first seven terms of theits first twenty terms.same AP is 167. If the sum of the first ten terms of this AP is 235, find the sum of first twenty terms
03:25View SolutionThe sum of the first sixteen terms of an AP is 112 and the sum of its next fourteen terms is 518 .Find the AP
05:30View SolutionThe sum of the first five terms of an AP and the sum of the first seven terms of the same AP is 167. If the sum first ten terms of this AP is 235, find the sum of its first twenty terms.
04:54View SolutionThe 12th term of an AP is -13 and the sum of its first four terms is 24. Find the sum of its first 10 terms.
03:29View SolutionIf the sum of first 7 terms of an AP is 49 and that of 17 terms is 289, find the sum of first n terms.
View SolutionIf the sum of first term of an A.P is 49 and that of 17 terms is 289. Find the sum of first "n" terms.
OR
The sum of the third and seyenth terms of an AP is 6 and their product is 8. find the sum of first sixteen terms of the A.P.03:27View Solutionयदि A. P. के पहले 6 पदों का योग 96 है और पहले 10 पदों का योग 240 है, तो उस A. P. के n पदों का योग ज्ञात कीजिए |
02:32View Solutionयदि A. P. के पहले 10 पदों का योग -60 और पहले 15 पदों का योग -165 है, तो उसके पहले n पदों का योग ज्ञात कीजिए |
05:41View SolutionIf the sum of first 7 terms of an AP is 49 and that of 17 terms is 289, find the sum of first n terms.
04:33View Solution

