vertical pole of length 3 m casts a shadow of 7 m and a tower casts a shadow of 28 m at a time. The height of tower is
10 m
12 m
14 m
16 m
The correct Answer is:A, B, C
To find the height of the tower based on the given information, we can use the concept of similar triangles. Here’s a step-by-step solution:
Step 1: Understand the Problem
We have a vertical pole of height 3 m that casts a shadow of 7 m. A tower casts a shadow of 28 m. We need to find the height of the tower.
Step 2: Identify the Triangles
Let’s denote:
- The vertical pole as triangle ABC, where:
- AB = height of the pole = 3 m
- BC = length of the shadow of the pole = 7 m
- The tower as triangle DEF, where:
- DE = height of the tower = H (unknown)
- EF = length of the shadow of the tower = 28 m
Step 3: Set Up the Proportions
Since the two triangles are similar (the angles are the same due to the sun's rays), we can set up the following proportion based on the corresponding sides:
ABDE=BCEF
Step 4: Substitute the Known Values
Substituting the known values into the proportion:
3H=728
Step 5: Simplify the Right Side
The fraction 728 can be simplified:
728=14
So, we have:
3H=14
Step 6: Cross-Multiply to Solve for H
Cross-multiplying gives:
3×4=1×H
This simplifies to:
12=H
Step 7: Conclusion
Thus, the height of the tower (H) is 12 m.
Final Answer:
The height of the tower is 12 m.
---
We have a vertical pole of height 3 m that casts a shadow of 7 m. A tower casts a shadow of 28 m. We need to find the height of the tower.
Let’s denote:
- The vertical pole as triangle ABC, where:
- AB = height of the pole = 3 m
- BC = length of the shadow of the pole = 7 m
- The tower as triangle DEF, where:
- DE = height of the tower = H (unknown)
- EF = length of the shadow of the tower = 28 m
Since the two triangles are similar (the angles are the same due to the sun's rays), we can set up the following proportion based on the corresponding sides:
Substituting the known values into the proportion:
The fraction 728 can be simplified:
Cross-multiplying gives:
Thus, the height of the tower (H) is 12 m.
The height of the tower is 12 m.
Topper's Solved these Questions
- TRIANGLEBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - TRIANGLEEXERCISE - Short Answer Type Questions-I
10 Videos
- TRIANGLEBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - TRIANGLEEXERCISE - Short Answer Type Questions-II
25 Videos
- TRIANGLEBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - TRIANGLEEXERCISE - Short Answer Type Questions-II
25 Videos
- SURFACE AREA AND VOLUME BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - SURFACE AREA AND VOLUME EXERCISE - PRACTICE TEST ( SECTION-D)
1 Videos
Similar Questions
At a certain time of a day a tree 5.4 m height casts a shadow of 9 m. If a pole casts a shadow of 13.5 m at the same time, the height of the pole is:
दिन के किसी समय में 5.4 मीटर ऊँचे पेड़ की 9 मीटर की परछाईं बनती है | यदि इसी समय एक खंभे की परछाईं 13.5 मीटर की है, तो खंभे की ऊंचाई ज्ञात करें |
View SolutionA vertical pole of length 6 m casts a shadow 4 m long on the ground and the same time a tower casts a shadow 28 m long. Find the height of the tower.
View Solution
Knowledge Check
A vertical stick 12 m long casts a shadow 8 m long on the ground. At the same time, a tower casts a shadow of 40 m long on the ground. The height of the tower is
A60 mB65 mC70 mD72 m
A vertical pole of length 7.5m casts a shadow 5 long on the ground and at the same time a tower casts a shadow 24 m long. Find the height of the tower.
View SolutionA vertical pole of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
View SolutionA vertical pole of length 8 m casts a shadow of 15 m long on the ground. At the same time, a tower casts a shadow 45 m long. Find the height of the tower.
View SolutionA vertical stick 10 cm long casts a shadow 8 cm long. At the same time a tower casts a shadow 30m long. Determine the height of the tower.
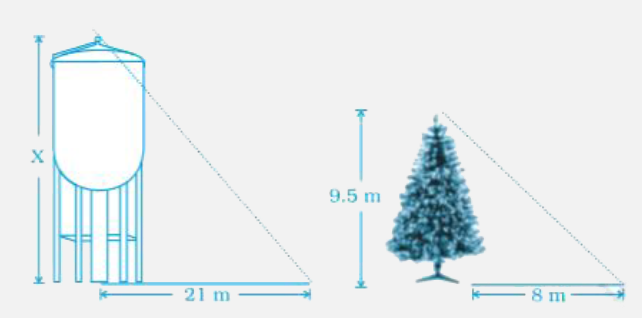
View SolutionA water tank casts a shadow 21 m long. A tree of height 9.5 m casts a shadow 8 m long at the same time. The lengths of the shadows are directly proprotional to their heights. Find the height of the tank.
View SolutionA vertical stick of length 6m casts a shadow 4m long on the ground and at the same time a tower casts a shadow 32m long. Find the height of the tower.
View SolutionA tree 6 m tall casts a shadow 4m long. At the same time if a tower casts the shadow 10m long then find the height of the tower.
View Solution
