A vertical flagstaff stands on a horizontal plane. From a point 100 m from its foot, the angle of elevation of its top is found to be 45∘. Find the height of the flagstaff.
The correct Answer is:100 m
To find the height of the flagstaff, we can use the concept of trigonometry, specifically the tangent function. Here is the step-by-step solution:
Step 1: Understand the problem
We have a vertical flagstaff and a point on the ground from where the angle of elevation to the top of the flagstaff is given. The distance from this point to the base of the flagstaff is also provided.
Step 2: Draw a diagram
Draw a right triangle where:
- The vertical side represents the height of the flagstaff (let's denote it as h).
- The horizontal side represents the distance from the point to the base of the flagstaff, which is 100 m.
- The angle of elevation from the point to the top of the flagstaff is 45∘.
Step 3: Set up the tangent function
Using the definition of the tangent function in a right triangle:
tan(θ)=oppositeadjacent
In our case, the angle θ=45∘, the opposite side is the height of the flagstaff h, and the adjacent side is the distance from the point to the base of the flagstaff, which is 100 m.
Thus, we can write:
tan(45∘)=h100
Step 4: Substitute the value of tan(45∘)
We know that:
tan(45∘)=1
So we can substitute this into our equation:
1=h100
Step 5: Solve for h
To find the height h, we multiply both sides of the equation by 100:
h=1×100
h=100 m
Conclusion
The height of the flagstaff is 100 meters.
---
We have a vertical flagstaff and a point on the ground from where the angle of elevation to the top of the flagstaff is given. The distance from this point to the base of the flagstaff is also provided.
Draw a right triangle where:
- The vertical side represents the height of the flagstaff (let's denote it as h).
- The horizontal side represents the distance from the point to the base of the flagstaff, which is 100 m.
- The angle of elevation from the point to the top of the flagstaff is 45∘.
Using the definition of the tangent function in a right triangle:
tan(θ)=oppositeadjacent
In our case, the angle θ=45∘, the opposite side is the height of the flagstaff h, and the adjacent side is the distance from the point to the base of the flagstaff, which is 100 m.
tan(45∘)=h100
We know that:
tan(45∘)=1
So we can substitute this into our equation:
1=h100
To find the height h, we multiply both sides of the equation by 100:
h=1×100
h=100 m
The height of the flagstaff is 100 meters.
Topper's Solved these Questions
- SOME APPLICATIONS OF TRIGONOMETRYBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - SOME APPLICATIONS OF TRIGONOMETRYEXERCISE - LONG ANSWER TYPE QUESTIONS
19 Videos
- SOME APPLICATIONS OF TRIGONOMETRYBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - SOME APPLICATIONS OF TRIGONOMETRYEXERCISE - PRACTICE-TEST (SECTION-A)
4 Videos
- SOME APPLICATIONS OF TRIGONOMETRYBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - SOME APPLICATIONS OF TRIGONOMETRYEXERCISE - PRACTICE-TEST (SECTION-D)
1 Videos
- REAL NUMBERSBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - REAL NUMBERSEXERCISE - LONG ANSWER TYPE QUESTION
15 Videos
- STATISTICSBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - STATISTICSEXERCISE - Practice -Test
5 Videos
Similar Questions
A vertical flagstaff stands on a horizontal plane. From a point 100 m from its foot, the angle of elevation the its top is 30°. Find the height of the flqgstaf.
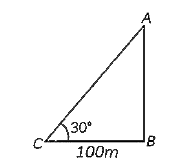
View SolutionA person standing at a distance of 90 m from a church observes the angle of elevation of its top to be 45∘ . Find the height of the chruch .
View Solution
Knowledge Check
A lamp post stands on a horizontal plane. From a point situated at a distance 150 m from its foot, the angle of elevation of the top is 30∘. What is the height of the lamp post?
A50mB50√3mC50√3mD100mA lamp post stands on a horizontal plane. From a point situated at a distance 150 m from its foot, the angle of elevation of the top is 30∘. What is the height of the lamp post?
A50mB50√3mC50√3mD100mA vertical pole stands on the level ground. From a point on the ground, 25m away from the foot of the pole , the angle of elevation of its top is found to be 60∘. Find the height of the pole.
A25√3B50√3C55√3D65√3
A tower stands vertically on the ground. From a point on the ground which is 30 m away from the foot of a tower, the angle of elevation of the top of the tower is found to be 45∘. Find the height of the tower.
View SolutionA 7 m long flagstaff is fixed on the top of a tower on the horizontal plane. From a point on the ground, the angles of elevation of the top and bottom of the flagstaff are 45∘ and 30∘ respectively. Find the height of the tower.
View SolutionA vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 5m. From a point on the ground the angles of elevation of the top and bottom of the flagstaff are 60∘ and 30∘ respectively. Find the height of the tower and the distance of the point from the tower. (Take √3=1.732)
View SolutionA tower stands vertically on the ground. From a point on the ground, which is 15m away from the foot of the tower, the angle of elevation of the top of the tower is found to be 60∘. Find the height of the tower.
View SolutionThe angle of elevation of the top of a tower standing on a horizontal plane from a point A is α. After walking a distance d towards the foot of the tower, the angle of elevation is found to be β. The height of the tower is
View Solution
