Find the radius of semicircle if its perimeter is 18 cm.
To find the radius of a semicircle given that its perimeter is 18 cm, we can follow these steps:
1. Understand the Perimeter of a Semicircle:
The perimeter (P) of a semicircle consists of the curved part and the diameter. The formula for the perimeter of a semicircle is:
P=πr+2r
where r is the radius of the semicircle.
2. Set Up the Equation:
We know from the problem that the perimeter is 18 cm. Therefore, we can set up the equation:
πr+2r=18
3. Factor Out the Radius:
We can factor out r from the left side of the equation:
r(π+2)=18
4. Solve for the Radius:
To find r, divide both sides of the equation by π+2:
r=18π+2
5. Substitute the Value of π:
We can use the approximate value of π as 227 for calculation:
r=18227+2
6. Simplify the Denominator:
Convert 2 into a fraction with a common denominator:
2=147
Therefore, the denominator becomes:
227+147=367
7. Rewrite the Equation:
Now substitute back into the equation for r:
r=18367=18×736
8. Calculate the Radius:
Simplifying gives:
r=12636=72=3.5 cm
Final Answer:
The radius of the semicircle is 3.5 cm.
---
The perimeter (P) of a semicircle consists of the curved part and the diameter. The formula for the perimeter of a semicircle is:
P=πr+2r
where r is the radius of the semicircle.
We know from the problem that the perimeter is 18 cm. Therefore, we can set up the equation:
πr+2r=18
We can factor out r from the left side of the equation:
r(π+2)=18
To find r, divide both sides of the equation by π+2:
r=18π+2
We can use the approximate value of π as 227 for calculation:
r=18227+2
Convert 2 into a fraction with a common denominator:
2=147
Therefore, the denominator becomes:
227+147=367
Now substitute back into the equation for r:
r=18367=18×736
Simplifying gives:
r=12636=72=3.5 cm
The radius of the semicircle is 3.5 cm.
Topper's Solved these Questions
- AREAS RELATED TO CIRCLESBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - AREAS RELATED TO CIRCLESEXERCISE - SHORT ANSWER TYPE II QUESTIONS
20 Videos
- AREAS RELATED TO CIRCLESBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - AREAS RELATED TO CIRCLESEXERCISE - LONG ANSWER TYPE QUESTIONS
10 Videos
- AREAS RELATED TO CIRCLESBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - AREAS RELATED TO CIRCLESEXERCISE - PRACTICE-TEST ( AREAS RELATED TO CIRCLES ) SECTION-D
1 Videos
- ARITHMETIC PROGRESSION BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ARITHMETIC PROGRESSION EXERCISE - PRACTICE TEST (SECTION D)
1 Videos
Similar Questions
Knowledge Check
The area of a triangle is 15 sq cm and the radius of its incircle is 3 cm. Its perimeter is equal to:
एक त्रिभुज का क्षेत्रफल 15 वर्ग सेमी है और इसके वृत्त की त्रिज्या 3 सेमी है। इसकी परिधि कितनी है?A12 cmB5 cmC10 cmD20 cmIn a triangle ABC, AB + BC = 12 cm, BC + CA = 14 cm and CA + AB = 18 cm. Find the radius of the circle (in cm) which has the same perimeter as the triangle.
A92B112C52D72In a triangle ABC,AB+BC=12cm,BC+CA=14cmand CA+AB=18cm. Find the radius of the circle (in cm) which has the same perimeter as the triangle.
A52B72C92D112
Find the area and the perimeter of the semicircle whose radius is 14 cm.
View SolutionFind the area and the perimeter of the semicircle whose radius is 14 cm.
View SolutionFind the perimeter (in cm) of semicircle of radius 28 cm.
View SolutionFind the area (in cm2) of a semicircle of radius 21 cm.
View SolutionThe figure below is made up of an isosceles triangle and a semicircle. Find the perimeter of the figure.
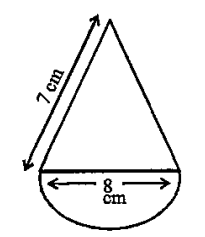
View Solution
