Which of the following sets are finite or infinite?Justify.
8. The set of all the points on the circumfrence of the circle.
The correct Answer is:Infinite set because circle is a collection of infinite points whose distances from the centre is constant called radius.
To determine whether the set of all points on the circumference of a circle is finite or infinite, we can follow these steps:
1. Understanding the Circle:
A circle is defined as the set of all points that are at a fixed distance (radius) from a central point (the center of the circle).
2. Defining the Set:
Let’s denote the set of all points on the circumference of a circle with radius r and center at point O as S. Thus, S={P∣distance(P,O)=r}.
3. Analyzing the Points:
The circumference of a circle is a continuous curve. This means that between any two points on the circumference, there are infinitely many other points. For instance, between any two points A and B on the circle, you can always find another point C such that A, C, and B are all distinct points on the circumference.
4. Conclusion:
Since there are infinitely many points between any two points on the circumference, we conclude that the set S is not countable. Therefore, the set of all points on the circumference of a circle is an infinite set.
Final Answer:
The set of all points on the circumference of a circle is an infinite set.
---
A circle is defined as the set of all points that are at a fixed distance (radius) from a central point (the center of the circle).
Let’s denote the set of all points on the circumference of a circle with radius r and center at point O as S. Thus, S={P∣distance(P,O)=r}.
The circumference of a circle is a continuous curve. This means that between any two points on the circumference, there are infinitely many other points. For instance, between any two points A and B on the circle, you can always find another point C such that A, C, and B are all distinct points on the circumference.
Since there are infinitely many points between any two points on the circumference, we conclude that the set S is not countable. Therefore, the set of all points on the circumference of a circle is an infinite set.
The set of all points on the circumference of a circle is an infinite set.
Topper's Solved these Questions
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - SETS AND FUNCTIONSEXERCISE - SHORT ANSWER TYPE QUESTIONS ( 2 MARKS)3videos
SETS AND FUNCTIONS
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - SETS AND FUNCTIONSEXERCISE - SHORT ANSWER TYPE QUESTIONS(4 MARKS)17videos
SETS AND FUNCTIONS
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - SEQUENCES AND SERIES EXERCISE - SECTION-D (LONG ANSWER TYPE QUESTIONS )19videos
SEQUENCES AND SERIES
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - STATISTICSEXERCISE - Section - D (Long Answer Type-II Questions) (6 Mark)10videos
STATISTICS
Similar Questions
Knowledge Check
- Question 1 - Select One
Which of the following is an infinite set ?
A{x:x is a prime, x<10}B{x:x is a vowel in the word MATHEMATICS}C{x:x is a natural number, 2015<x<2016}D{x:x∈Z,x is a non-negative integer} - Question 2 - Select One
Which of the following set of points are collinear?
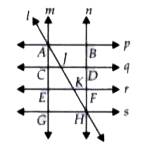 AA.J.K.HBA.J.E.GCB.D. H. EDA.J. K. F
AA.J.K.HBA.J.E.GCB.D. H. EDA.J. K. F - Question 3 - Select One
Which of the following is NOT an infinite set ?
Aset of rational numbers between any two number on number lineBset of irrational numbers between any two numbers on number lineCset of rationl numbers between 0.¯9 and 1.DNone of these
Which one of the following is an infinite set ?
View SolutionIn which of the following sets all are vectors
View SolutionWhich of the following set has all the coloured ions ?
View SolutionWhich of the following set is not a null set ?
View SolutionWhich of the following set of points are non-collinear?
View Solution

