Show the graph of the solution of 2x - 3 > X-5 on number line.
To solve the inequality 2x−3>x−5 and graph the solution on a number line, we can follow these steps:
Step 1: Rearrange the inequality
We start with the inequality:
2x−3>x−5
To isolate x, we will move the x terms to one side and the constant terms to the other side. We can do this by subtracting x from both sides:
2x−x−3>−5
This simplifies to:
x−3>−5
Step 2: Add 3 to both sides
Next, we will add 3 to both sides to further isolate x:
x−3+3>−5+3
This simplifies to:
x>−2
Step 3: Interpret the solution
The solution x>−2 means that x can take any value greater than −2. This is an open interval, which we can express in interval notation as:
(−2,∞)
Step 4: Graph the solution on a number line
To represent this solution on a number line:
1. Draw a horizontal line to represent the number line.
2. Mark the point −2 on the number line.
3. Since −2 is not included in the solution, we will use an open circle at −2.
4. Shade the line to the right of −2 to indicate that all values greater than −2 are included in the solution.
Final Representation
The graph will show an open circle at −2 and a shaded line extending to the right towards infinity.
---
We start with the inequality:
2x−3>x−5
2x−x−3>−5
x−3>−5
Next, we will add 3 to both sides to further isolate x:
x−3+3>−5+3
x>−2
The solution x>−2 means that x can take any value greater than −2. This is an open interval, which we can express in interval notation as:
(−2,∞)
To represent this solution on a number line:
1. Draw a horizontal line to represent the number line.
2. Mark the point −2 on the number line.
3. Since −2 is not included in the solution, we will use an open circle at −2.
4. Shade the line to the right of −2 to indicate that all values greater than −2 are included in the solution.
The graph will show an open circle at −2 and a shaded line extending to the right towards infinity.
Topper's Solved these Questions
- LINEAR INEQUALITIESBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - LINEAR INEQUALITIESEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS (Fill in the blanks )
5 Videos
- LINEAR INEQUALITIESBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - LINEAR INEQUALITIESEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS(MCQ)
9 Videos
- LIMITS AND DERIVATIVES BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - LIMITS AND DERIVATIVES EXERCISE - LONG ANSWER TYPE QUESTIONS
33 Videos
- MATHEMATICAL REASONINGBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - MATHEMATICAL REASONINGEXERCISE - SECTION-B SHORT ANSWER TYPE QUESTIONS
5 Videos
Similar Questions
Knowledge Check
The graph of the solution on number line of the inequality3x−2<2x+1is
A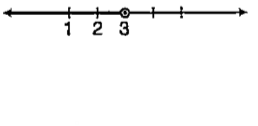 B
B C
C D
D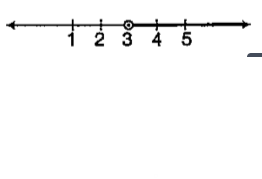
Solve the inequalities and show the graph of the solution in each case on number line : 5x−3≥3x−5
View SolutionSolve the inequalities and show the graph of the solution in each case on number line : x2≥(5x−2)3−(7x−3)5
View SolutionSolve the inequalities and show the graph of the solution in each case on number line : 3x−2<2x+1
View SolutionSolve the inequalities and show the graph of the solution in each case on number line : 3(1x)<2(x+4)
View SolutionSolve the following inequalities and show the graph of the solution set on number line:
(i) 3x−2<2x+1
(ii) 5x−3≥3x−5.
View SolutionSolve the following inequalities and show the graph of the solution set on number line:
Solve:
(a) −12x>30
(b) 30x<200, when:
(i) x in a natural number.
(ii) x is an integer.
View SolutionSolve 3x+5<x−7, when:
(i) x is an integer (ii) x is a real number.
Show graph of the solution set on the number line in both cases.
View Solution
