In the above question, change in internal energy of gas is
−2660.23J
−2777.23J
−2767.23J
−2600J
The correct Answer is:C
Change in internal energy ΔU=nCvΔT,n No of moles Cv=Rγ−1∴ΔU=nRγ−1ΔT
ΔU=2×8.31×(189−300)53−1=−2767.23J
Topper's Solved these Questions
- THERMODYNAMICS BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - THERMODYNAMICS EXERCISE - NUMERICALS
14 Videos
- ROTATIONAL MOTION BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ROTATIONAL MOTION EXERCISE - MULTIPLE CHOICE QUESTIONS
20 Videos
- WORK, ENERGY AND POWERBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - WORK, ENERGY AND POWEREXERCISE - MCQ
20 Videos
Similar Questions
Knowledge Check
In the above question, change in internal energy of gas is
A−2660.23JB−2777.23JC−2767.23JD−2600JIn an adiabatic process 90 J of work is done on the gas. The change in internal energy of the gas is
A−90jB+90jC0 jDDepends on initial temperatureThe change in the internal energy of a substance
AIncrease with increase in temperatureBDecrease with increase in temperatureCCan be calculated the relation E=mc2DRemains unaffected with change in temperature
the change in internal energy of a ayatem depends on
View SolutionOne mole of an ideal diatomic gas undergoes a transition from A to B along a path AB as shown in the figure. The change in internal energy of the gas during the transition is
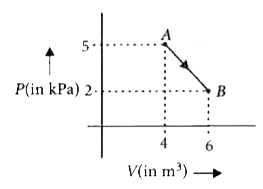
View SolutionOne mole of an ideal diatomic gas undergoes a transition from A to B along a path AB as shown in the figure,
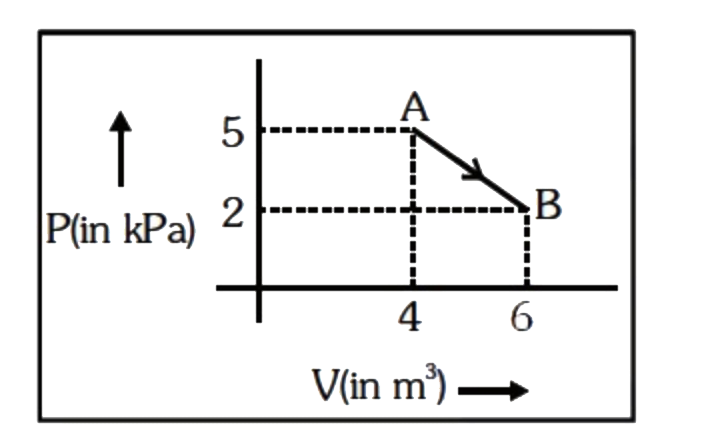
The change in internal energy of the gas during the transition is :
View SolutionIn thermodynamic process, 200 Joules of heat is given to a gas and 100 Joules of work is also done on it. The change in internal energy of the gas is
View SolutionIn an adiabatic expansion of a gas initial and final temperatures are T1and T2 respectively, then the change in internal energy of the gas is
View Solution
