Let g(x)=1+x−[x]andf(x)={−1,x<00,x=0f,x>0. Then for all x,f(g(x)) is equal to (where [.] represents the greatest integer function). (a) x (b) 1 (c) f(x) (d) g(x)
To solve the problem, we need to evaluate f(g(x)) where g(x)=1+x−(x) and f(x) is defined as follows:
- f(x)=−1 for x<0
- f(x)=0 for x=0
- f(x)=1 for x>0
Step 1: Understand the function g(x)
The function g(x) can be rewritten using the definition of the greatest integer function. We know that:
g(x)=1+x−(x)
This can be interpreted as:
g(x)=1+{x}
where {x}=x−(x) is the fractional part of x. The fractional part {x} always lies in the range (0,1).
Step 2: Analyze the output of g(x)
Since {x} is always non-negative and less than 1, we can deduce:
g(x)=1+{x}⟹g(x)∈(1,2)
This means that for any real number x, g(x) will always be greater than or equal to 1.
Step 3: Evaluate f(g(x))
Now, we need to evaluate f(g(x)). Since we have established that g(x) is always in the interval (1,2), we can apply the definition of f(x):
- For g(x)≥1, we have g(x)>0.
- Therefore, according to the definition of f(x):
f(g(x)) = 1 \quad \text{(since g(x) > 0 )}
Conclusion
Thus, for all x, f(g(x))=1.
Final Answer
The correct option is (b) 1.
---
- f(x)=0 for x=0
- f(x)=1 for x>0
g(x)=1+x−(x)
This can be interpreted as:
g(x)=1+{x}
where {x}=x−(x) is the fractional part of x. The fractional part {x} always lies in the range (0,1).
g(x)=1+{x}⟹g(x)∈(1,2)
This means that for any real number x, g(x) will always be greater than or equal to 1.
- Therefore, according to the definition of f(x):
f(g(x)) = 1 \quad \text{(since g(x) > 0 )}
Similar Questions
Knowledge Check
Let g(x)=1+x−[x]andf(x)=⎧⎪⎨⎪⎩−1,x<00,x=01,x>0, then for all x,f[g(x)] is equal to
A0B1CxDf(x)If f(x)=Sgn x and g(x)=1+x-[x], then for all x, f(g(x)) is equal to :
A0B1CxDf(x)Let g(x)=1+x-[x] and
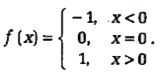 Then for all x,f {g(x)} is equal to AxB1Cf(x)Dg(x)
Then for all x,f {g(x)} is equal to AxB1Cf(x)Dg(x)
If f(x)={gx,x<0anda[x],a∈R−{0},x≥0, where [.] denotes the greatest integer function. The f(x)
View SolutionLet g(x) = 1 + x – [x] and f(x)=⎧⎪⎨⎪⎩−1ifx<00ifx=01ifx>0 then Aax,fog(x) equals
(where [ * ] represents greatest integer function).
View Solutioniff(x)={1−|x|1+xx≠−11x=−1then f([2x]) , where [.] represents the greatest integer function , is
View SolutionLet g(x) = x - [x] - 1 and f(x)=⎧⎪⎨⎪⎩−1, x<00, x=01, x>0 [.] represents the greatest integer function then for all x, f(g(x)) = .
View SolutionLet f(x)=|x|andg(x)=[x], (where [.] denotes the greatest integer function) Then, (fog)'(−1) is
View Solution
