From a point P(3, 3) on the circle x2+y2=18 , two chords PQ and PR each of 2 units length are drawn on this circle. The value of cos (∠QPR) is equal to
13√2
−89
√23
−49
The correct Answer is:B
To solve the problem, we need to find the value of cos(QPR) given the point P(3, 3) on the circle defined by the equation x2+y2=18 and two chords PQ and PR, each of length 2 units.
1. Verify the Point P(3, 3) on the Circle:
The equation of the circle is x2+y2=18.
Substitute x=3 and y=3:
32+32=9+9=18
Since this is true, point P(3, 3) lies on the circle.
Hint: Always verify if the given point lies on the circle by substituting its coordinates into the circle's equation.
2. Identify the Radius of the Circle:
The radius r of the circle can be calculated from the equation:
r=√18=3√2
Hint: The radius can be found by taking the square root of the right side of the circle's equation.
3. Draw the Chords PQ and PR:
We know that the lengths of both chords PQ and PR are 2 units. Let O be the center of the circle (0, 0). The lengths of OP, OQ, and OR (the radius) are all equal to 3√2.
4. Apply the Cosine Rule in Triangle OQP:
In triangle OQP, we have:
- OP = 3√2 (radius)
- OQ = 3√2 (radius)
- PQ = 2 (length of the chord)
Using the cosine rule:
PQ2=OP2+OQ2−2⋅OP⋅OQ⋅cos(QOP)
Substituting the known values:
22=(3√2)2+(3√2)2−2⋅(3√2)⋅(3√2)⋅cos(QOP)
Simplifying:
4=18+18−18⋅cos(QOP)
4=36−18⋅cos(QOP)
Rearranging gives:
18⋅cos(QOP)=36−4=32
cos(QOP)=3218=169
Hint: The cosine rule relates the lengths of the sides of a triangle to the cosine of one of its angles.
5. Find the Angle QPR:
Since QPR is an angle formed by the two chords PQ and PR, and both chords are equal in length, we can use the property of the cosine of angles:
cos(QPR)=cos(2⋅QOP)
Using the double angle formula:
cos(2θ)=2cos2(θ)−1
Substituting cos(QOP):
cos(QPR)=2(169)2−1
=2⋅25681−1=51281−1=512−8181=43181
Hint: The double angle formula for cosine is useful when dealing with angles formed by equal chords.
6. Final Result:
Therefore, the value of cos(QPR) is 43181.
The equation of the circle is x2+y2=18.
Substitute x=3 and y=3:
32+32=9+9=18
Since this is true, point P(3, 3) lies on the circle.
The radius r of the circle can be calculated from the equation:
r=√18=3√2
We know that the lengths of both chords PQ and PR are 2 units. Let O be the center of the circle (0, 0). The lengths of OP, OQ, and OR (the radius) are all equal to 3√2.
In triangle OQP, we have:
- OP = 3√2 (radius)
- OQ = 3√2 (radius)
- PQ = 2 (length of the chord)
PQ2=OP2+OQ2−2⋅OP⋅OQ⋅cos(QOP)
Substituting the known values:
22=(3√2)2+(3√2)2−2⋅(3√2)⋅(3√2)⋅cos(QOP)
Simplifying:
4=18+18−18⋅cos(QOP)
4=36−18⋅cos(QOP)
Rearranging gives:
18⋅cos(QOP)=36−4=32
cos(QOP)=3218=169
Since QPR is an angle formed by the two chords PQ and PR, and both chords are equal in length, we can use the property of the cosine of angles:
cos(QPR)=cos(2⋅QOP)
Using the double angle formula:
cos(2θ)=2cos2(θ)−1
Substituting cos(QOP):
cos(QPR)=2(169)2−1
=2⋅25681−1=51281−1=512−8181=43181
Therefore, the value of cos(QPR) is 43181.
Topper's Solved these Questions
Similar Questions
From the point A(0, 3) on the circle x2+4x+(y−3)2=0, a chord AB is drawn and extended from point B to a point M such that AM = 2AB. The perimeter of the locus of M is pπ units. Then, the value of p is
View Solution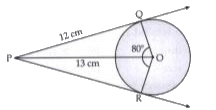
A point P is 13 cm from the centre of the circle. The two tangent PQ and PR are drawn from the point P, The length of the tangent drawn from P to the circle is 12 cm.
∠PQO is equal to ………. .
View Solution
Knowledge Check
From a point P(3, 3) on the circle x2+y2=18 two chords PQ and PR each of he length 2 units are drawn on this circle. Then, the value of the length PM is equal to (where, M is the midpoint of the line segment joining Q and R)
A13√2 unitsB12 unitsC√23 unitsD49 unitsFrom a point A(1, 1) on the circle x2+y2−4x−4y+6=0 two equal chords AB and AC of length 2 units are drawn. The equation of chord BC, is
A4x+3y-12=0Bx+y=4C3x+4y=4Dx+y=6The two lines through (2,3) from which the circle x2+y2=25 intercepts chords of length 8 units have equations
A2x+3y=13,x+5y=17By=3,12x+5y=39Cx=2,9x−11y=51Dnone of these
Tangents are drawn from points on the line x+2y=8 to the circle x2+y2=16. If locus of mid-point of chord of contacts of the tangents is a circles S, then radius of circle S will be
View SolutionIf a chord of contact of tangents drawn from a point P with respect to the circle x2+y2=9 is x=2, then area, in square units, of triangle formed by tangents drawn from P to the circle and their chord of contact is equal to
View SolutionTangents drawn from the point (4,4) to the circle
x2+y2−2x−2y−7=0 meets the circle at A andB then the length of chord AB is equal to
View SolutionTangents drawn from the point P(1,8) to the circle x2+y2−6x−4y−11=0 touch the circle at the points A and B. The equation of the circumcircle of the triangle PAB is:
View SolutionTangents drawn from the point P(1,8) to the circle x2+y2−6x−4y−11=0 touch the circle at the points A and B. The equation of the circumcircle of the triangle PAB is:
View Solution