In Young's double - slit experiment intensity at a point is (3/4)th of the maximum intensity. The possible angular position of this point is
sin−1(λ3d)
sin−1(λ2a)
sin−1(λ6d)
sin−1(λ4d)
The correct Answer is:C
To solve the problem step by step, we will analyze the situation in Young's double-slit experiment where the intensity at a point is given as 34 of the maximum intensity. We need to find the possible angular position of this point.
Step 1: Understand the relationship between intensity and phase difference
In Young's double-slit experiment, the intensity I at a point on the screen can be expressed in terms of the maximum intensity Imax and the phase difference ΔΦ as follows:
I=Imaxcos2(ΔΦ2)
Step 2: Set up the equation for the given intensity
We are given that the intensity I is 34 of the maximum intensity Imax:
I=34Imax
Substituting this into the intensity equation gives:
34Imax=Imaxcos2(ΔΦ2)
Step 3: Simplify the equation
Dividing both sides by Imax (assuming Imax≠0):
34=cos2(ΔΦ2)
Step 4: Solve for the phase difference
Taking the square root of both sides:
cos(ΔΦ2)=±√34=±√32
This gives us two possible angles:
ΔΦ2=π6+nπorΔΦ2=5π6+nπ(n∈Z)
Thus, the phase difference ΔΦ can be:
ΔΦ=π3+2nπorΔΦ=5π3+2nπ
Step 5: Relate phase difference to path difference
The phase difference ΔΦ is also related to the path difference Δx by:
ΔΦ=2πλΔx
The path difference Δx can be expressed as:
Δx=dsinθ
where d is the distance between the slits and θ is the angle from the central maximum.
Step 6: Substitute and solve for θ
Substituting for Δx:
ΔΦ=2πλ(dsinθ)
Setting this equal to the two possible values of ΔΦ:
1. For ΔΦ=π3:
π3=2πλ(dsinθ)⟹sinθ=λ6d
2. For ΔΦ=5π3:
5π3=2πλ(dsinθ)⟹sinθ=5λ6d
Step 7: Conclusion
The possible angular positions θ can be found using:
θ=sin−1(λ6d)orθ=sin−1(5λ6d)
In Young's double-slit experiment, the intensity I at a point on the screen can be expressed in terms of the maximum intensity Imax and the phase difference ΔΦ as follows:
I=Imaxcos2(ΔΦ2)
We are given that the intensity I is 34 of the maximum intensity Imax:
I=34Imax
Substituting this into the intensity equation gives:
34Imax=Imaxcos2(ΔΦ2)
Dividing both sides by Imax (assuming Imax≠0):
34=cos2(ΔΦ2)
Taking the square root of both sides:
cos(ΔΦ2)=±√34=±√32
This gives us two possible angles:
ΔΦ2=π6+nπorΔΦ2=5π6+nπ(n∈Z)
Thus, the phase difference ΔΦ can be:
ΔΦ=π3+2nπorΔΦ=5π3+2nπ
The phase difference ΔΦ is also related to the path difference Δx by:
ΔΦ=2πλΔx
The path difference Δx can be expressed as:
Δx=dsinθ
where d is the distance between the slits and θ is the angle from the central maximum.
Substituting for Δx:
ΔΦ=2πλ(dsinθ)
Setting this equal to the two possible values of ΔΦ:
1. For ΔΦ=π3:
π3=2πλ(dsinθ)⟹sinθ=λ6d
2. For ΔΦ=5π3:
5π3=2πλ(dsinθ)⟹sinθ=5λ6d
The possible angular positions θ can be found using:
θ=sin−1(λ6d)orθ=sin−1(5λ6d)
Topper's Solved these Questions
Similar Questions
Youngs Double slit experiment | variation of intensity on screen
View SolutionThe intensity of the light coming from one of the slits in a Young's double slit experiment is double the intensity from the other slit. Find the ratio of the maximum intensity to the minimum intensity in the interference fringe pattern observed.
View Solution
Knowledge Check
In Young's double slit experiment intensity at a point is (14) of the maximum intersity. Angular position of this point is
Asin−1(λd)Bsin−1(λ2d)Csin−1(λ3d)Dsin−1(λ4d)In Young's double slit experiment intensity at a point is (14) of the maximum intersity. Angular position of this point is
Asin−1(λd)Bsin−1(λ2d)Csin−1(λ3d)Dsin−1(λ4d)In Young's double slit experiment intensity at a point is (14) of the maximum intersity. Angular position of this point is
Asin−1(λ/3d)Bsin−1(λ/2d)Csin−1(λ/4d)Dsin−1(λ/d)
In Young's double slit experiment, the intensity of central maximum is I. What will be the intensity at the same place if one slit is closed ?
View SolutionIn young's double slit experiment relative intensity at a point on the screen may be defined as ratio of intensity at that point to the maximum intensity on the screen. Light of wavelength 7500∘A A passing through a double slit, produces interference pattern of relative intensity variation as shown in Fig. θ on horizontal axis represents the angular position of a point on the screen
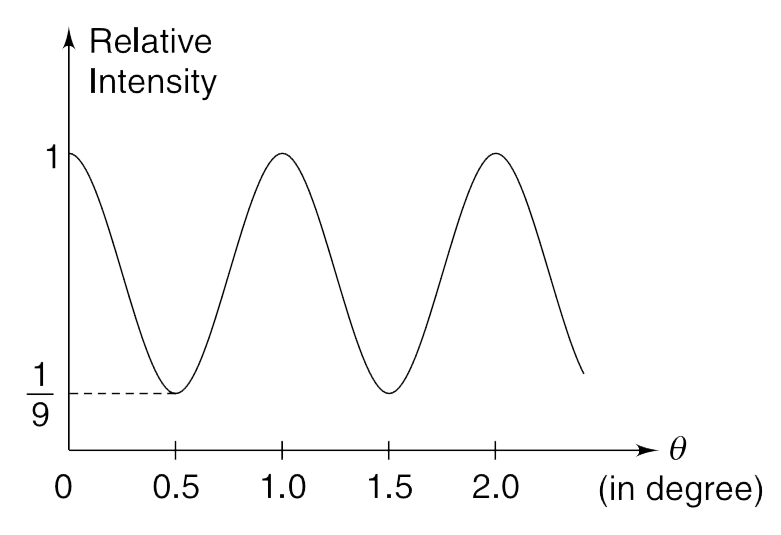
(a) Find separation d between the slits.
(b) Find the ratio of amplitudes of the two waves producing interference pattern on the screen.
View SolutionIn a Young's double slit experiment, the central point on the screen is
View SolutionIn Young's double-slit experiment, the intensity at a point P on the screen is half the maximum intensity in the interference pattern. If the wavelength of light used is λ and d is the distance between the slits, the angular separation between point P and the center of the screen is
View SolutionIn Young's double slit experiment the intensity of light at a point on the screen where the path difference λ is K. The intensity of light at a point where the path difference is λ6 [λ is the wavelength of light used] is
View Solution
