A particle is projected directly along a rough plane of inclination θ with velocity u. If after coming to the rest the particle returns to the starting point with velocity v, the coefficient of friction between the partice and the plane is
u2v2tanθ
u2−v2u2+v2tanθ
v2u2tanθ
u2+v2u2−v2tanθ
The correct Answer is:B
To solve the problem of finding the coefficient of friction between a particle and a rough inclined plane, we can follow these steps:
1. Identify Forces Acting on the Particle:
- When the particle is projected up the incline, the forces acting on it are:
- Gravitational force component down the incline: mgsinθ
- Normal force: N=mgcosθ
- Frictional force acting down the incline: Ff=μN=μmgcosθ
2. Write the Equation of Motion for Upward Motion:
- The net force acting on the particle when it moves up the incline is:
Fnet=−mgsinθ−μmgcosθ
- According to Newton's second law, this can be expressed as:
ma=−mgsinθ−μmgcosθ
- Dividing by m:
a=−gsinθ−μgcosθ
3. Use the Kinematic Equation:
- The kinematic equation for the upward motion is:
0=u2+2as
- Substituting for a:
0=u2+2(−gsinθ−μgcosθ)s
- Rearranging gives:
u2=2gs(sinθ+μcosθ)(Equation 1)
4. Analyze the Downward Motion:
- When the particle returns down the incline, the forces acting on it are:
- Gravitational force component down the incline: mgsinθ
- Frictional force acting up the incline: Ff=μmgcosθ
- The net force while moving down is:
Fnet=mgsinθ−μmgcosθ
- Thus, the acceleration is:
a=gsinθ−μgcosθ
5. Use the Kinematic Equation for Downward Motion:
- The kinematic equation for the downward motion is:
v2=0+2as
- Substituting for a:
v2=2(gsinθ−μgcosθ)s
- Rearranging gives:
v2=2gs(sinθ−μcosθ)(Equation 2)
6. Divide Equation 1 by Equation 2:
- Dividing the two equations:
u2v2=sinθ+μcosθsinθ−μcosθ
- Cross-multiplying gives:
u2(sinθ−μcosθ)=v2(sinθ+μcosθ)
7. Rearranging to Solve for μ:
- Rearranging terms:
u2sinθ−u2μcosθ=v2sinθ+v2μcosθ
- Collecting μ terms:
u2sinθ−v2sinθ=u2μcosθ+v2μcosθ
- Factoring out μ:
(u2−v2)sinθ=μ(u2+v2)cosθ
- Solving for μ:
μ=(u2−v2)sinθ(u2+v2)cosθ
Final Answer:
The coefficient of friction μ between the particle and the plane is given by:
μ=(u2−v2)sinθ(u2+v2)cosθ
- When the particle is projected up the incline, the forces acting on it are:
- Gravitational force component down the incline: mgsinθ
- Normal force: N=mgcosθ
- Frictional force acting down the incline: Ff=μN=μmgcosθ
- The net force acting on the particle when it moves up the incline is:
Fnet=−mgsinθ−μmgcosθ
- According to Newton's second law, this can be expressed as:
ma=−mgsinθ−μmgcosθ
- Dividing by m:
a=−gsinθ−μgcosθ
- The kinematic equation for the upward motion is:
0=u2+2as
- Substituting for a:
0=u2+2(−gsinθ−μgcosθ)s
- Rearranging gives:
u2=2gs(sinθ+μcosθ)(Equation 1)
- When the particle returns down the incline, the forces acting on it are:
- Gravitational force component down the incline: mgsinθ
- Frictional force acting up the incline: Ff=μmgcosθ
- The net force while moving down is:
Fnet=mgsinθ−μmgcosθ
- Thus, the acceleration is:
a=gsinθ−μgcosθ
- The kinematic equation for the downward motion is:
v2=0+2as
- Substituting for a:
v2=2(gsinθ−μgcosθ)s
- Rearranging gives:
v2=2gs(sinθ−μcosθ)(Equation 2)
- Dividing the two equations:
u2v2=sinθ+μcosθsinθ−μcosθ
- Cross-multiplying gives:
u2(sinθ−μcosθ)=v2(sinθ+μcosθ)
- Rearranging terms:
u2sinθ−u2μcosθ=v2sinθ+v2μcosθ
- Collecting μ terms:
u2sinθ−v2sinθ=u2μcosθ+v2μcosθ
- Factoring out μ:
(u2−v2)sinθ=μ(u2+v2)cosθ
- Solving for μ:
μ=(u2−v2)sinθ(u2+v2)cosθ
The coefficient of friction μ between the particle and the plane is given by:
μ=(u2−v2)sinθ(u2+v2)cosθ
Topper's Solved these Questions
Similar Questions
A particle is projected on a frictionless inclined plane of inclination 37∘ at an angle of projection 45∘ from the inclined plane as shown in the figure. If after the first collision from the plane, the particle returns to its point of projection, then what is the value of the reciprocal of the coefficient of restitution between the particle and the plane?
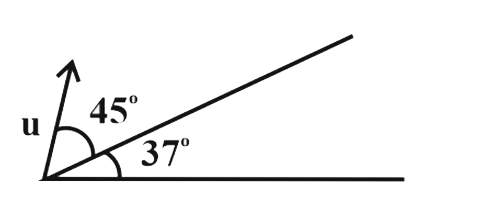
View SolutionA paricle is projected up from the bottom of an inlined plane of inclination α with velocity v0 If it returns to the points of projection after an elastic impact with the plane, find the total time of motion of the particle.
View Solution
Knowledge Check
A particle is projected up a 37∘ rough incline with velocity v0. If μ=1/2, the speed with which it returns back to the starting point is v. Then v/v0 is
A12B1√3C1√5D1√2A particle is projected up a 45∘ rough incline with a velocity v. The coeffciient of friciton is 0.5. The speed with which it returns back to the starting point is v'. Then v' /v is :
A√2/√3B1/√3C1/2D1/√2A particle is projected up a rough inclined plane of inclination θ and friction coefficient μ. If the time of ascent is half of the time of descent, the friction coefficient μ is equal to
A34tanθB35tanθC45tanθD12tanθ
A block starts moving up an inclined plane of inclination 30∘ with an initial velocity of v0 . It comes back to its initial position with velocity v02 . The value of the coefficient of kinetic friction between the block and the inclined plane is close to I1000 , The nearest integer to I is ____________ .
View SolutionA positively charged particle of mass m and charge q is projected on a rough horizontal x-y plane surface with z-axis in the vertically upward direction. Both electric and magnetic fields are acting in the region and given by →E=−E0ˆkand→B=−B0ˆk , respectively. The particle enters into the field at (a0,0,0) with velocity →v=v0ˆj. The particle starts moving in some curved path on the plane. If the coefficient of friction between the particle and the plane is μ. Then calculate the
(a) time when the particle will come to rest
(b) distance travelled by the particle when it comes to rest.

View SolutionA charged particle of mass m and charge q is projected on a rough horizontally xy− plane surface with z− axis in the vertically upward direction. Both electric and magnetic fields are acting in the region and given by →E=−E0ˆk and →B=−B0ˆk respectively. The particle enters into the field at (a,0,0) with velocity →v=υ0ˆj. The particle starts moving into a circular path on the plane. If the coefficient of friction between the particle and the plane is μ. Then calculate tha :

(a) time when the particle will come to rest
(b) time when the particle will hit the centre.
(c) distance travelled by the particle when it comes to rest.
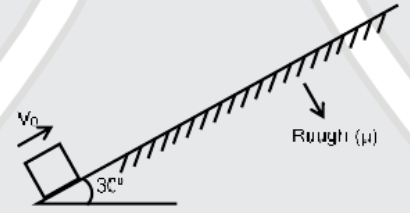
View SolutionA block starts going up a rough inclined plane with velocity V0 as shown in figure.After some time reaches to starting point again, with a velocity V02.Find coefficient of friction μ .Given g=10msec2.
View SolutionA particle is projected with velocity v at an angle of θ with horizontal. The average angular velocity of the particle from the point of projection to impact equals:
View Solution
