A storage tower supplies water, as shown in the figure. If P0 is the atmospheric pressure h = height of water level, g = acceleration due to gravity, ρ= density and v = velocity of flow in the horizontal pipe at B, then the pressure at B is -
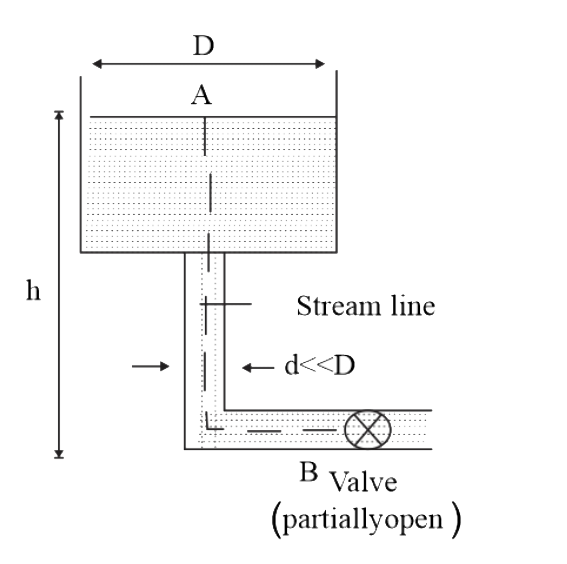
P0
P0+ρgh
P0+ρgh+12ρv2
P0+ρgh−12ρv2
The correct Answer is:D
Step by step video, text & image solution for A storage tower supplies water, as shown in the figure. If P_(0) is the atmospheric pressure h = height of water level, g = acceleration due to gravity, rho= density and v = velocity of flow in the horizontal pipe at B, then the pressure at B is - by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
The pressure at a depth h in a liquid of density d is given by pressure = __ , where g is the acceleration due to gravity.
View SolutionA small air bubble of radius r in water is at depth h below the water surface. If P0 is the atmospheric pressure, ρ is the density of water and T is the surface tension of water, what is the pressure inside the bubble?
View Solution
Knowledge Check
- Question 1 - Select One
The absolute pressure at a depth h below the surface of a liquid of density ρ is [Given Pa = atmospheric pressure, g = acceleration due to gravity]
AρghBPa+ρghCPa−ρghDPa2ρgh - Question 2 - Select One
A small air bubble of radius r in water is at a depth h (r<<h). If Po is the atmospheric pressure, ρ is the density of water and T is the surface tension of water, the excess pressure inside the bubble over the pressure outside it is
Aρgh+4TrB4TrC2TrDρgh+2Tr - Question 3 - Select One
According to Bernoulli's theorem pd+v22+gh = constant is (P is pressure, d is density, h is height, v is velocity and g is acceleration due to gravity)
A[M0L0T0]B[M0LT0]C[M0L2T−2]D[M0L2T−4]
A liquid of density ρ is in a vessel rotating with angular velocity ω as shown in figure. If P0 is the atmospheric pressure, find pressure at a radial distance r from the axis.
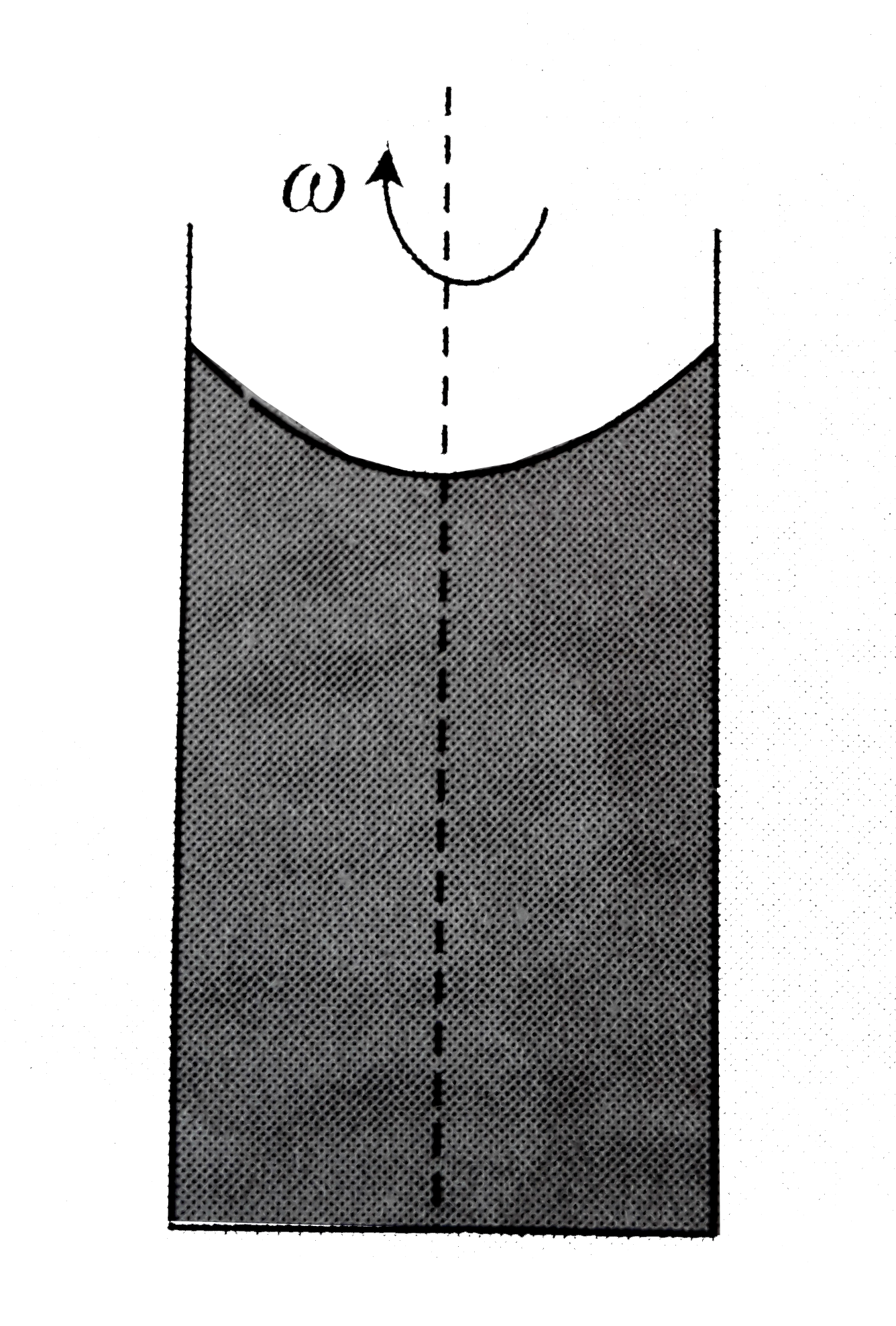 .View Solution
.View SolutionThe velocity of water wave v may depend on their wavelength λ, the density of water ρ and the acceleration due to gravity g. The method of dimensions gives the relation between these quantities as
View SolutionA tube of uniform cross section is used to siphon water from a vessel V as shown in the figure. The pressure over the open end of water in the vessel is atmospheric pressure (P0). The height of the tube above and below the water level in the vessel are h1 and h2, respectively.

Determine the velocity vB of the water issuing out at B.View SolutionA tube of uniform cross section is used to siphon water from a vessel V as shown in the figure. The pressure over the open end of water in the vessel is atmospheric pressure (P0). The height of the tube above and below the water level in the vessel are h1 and h2, respectively.
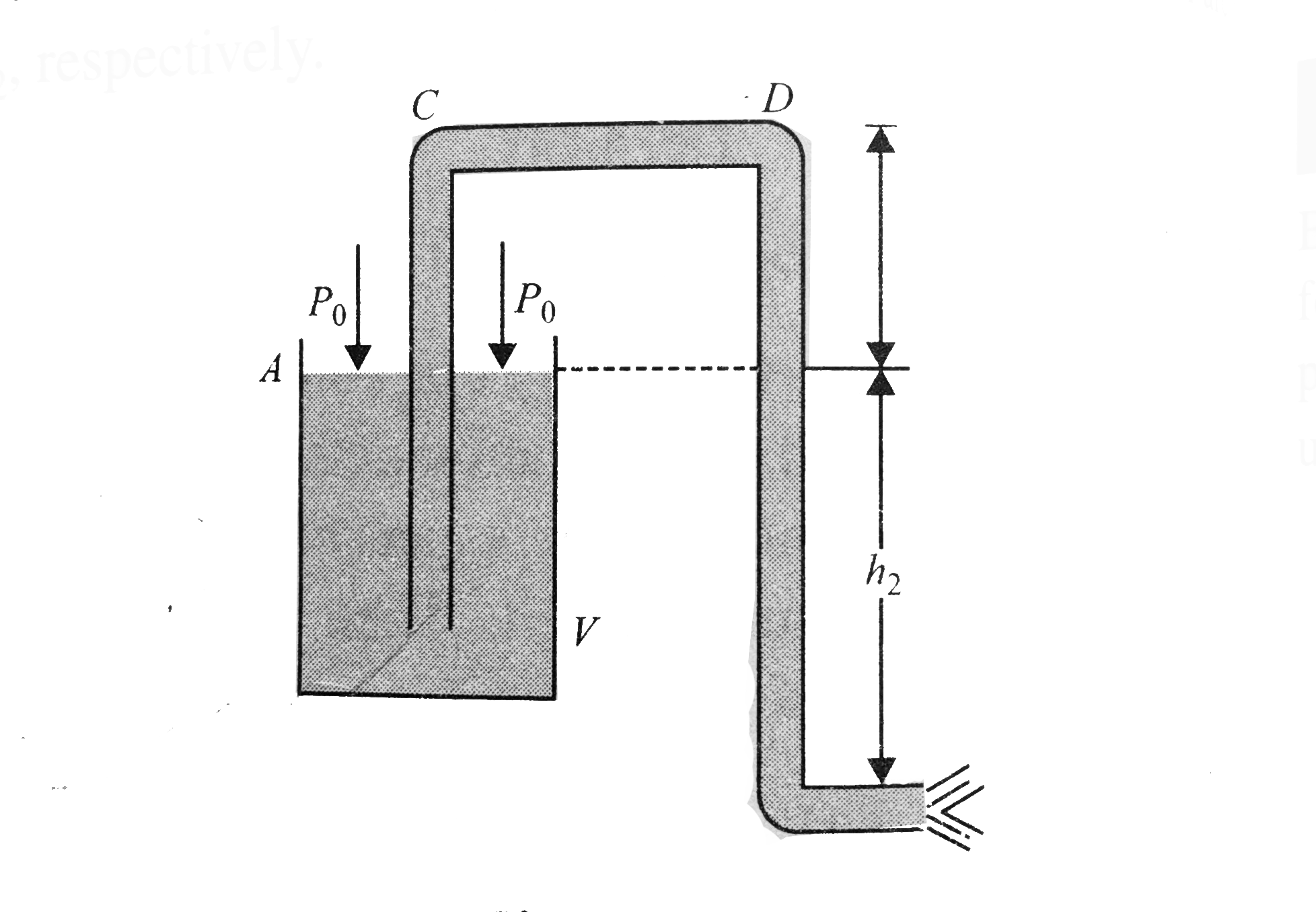
Given h1=h2=3.0m, the gauge pressure of water in the highest level CD of the tube will beView SolutionA tube of uniform cross section is used to siphon water from a vessel V as shown in the figure. The pressure over the open end of water in the vessel is atmospheric pressure (P0). The height of the tube above and below the water level in the vessel are h1 and h2, respectively.
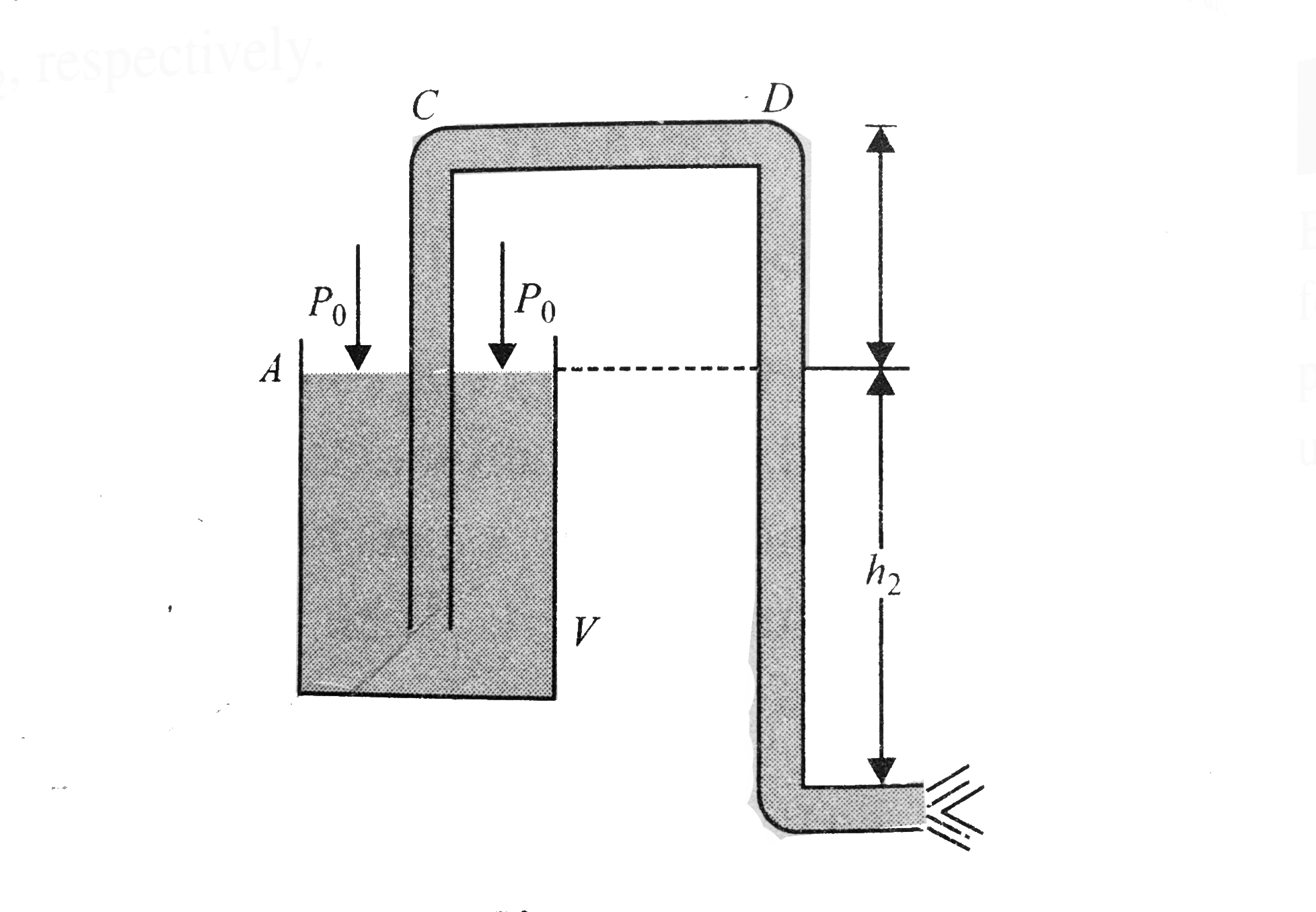
If h1=h2=3.0m, the maximum value of h1, for which the siphon will work will beView Solution

