The viscosity η of a gas depends on the long - range attractive part of the intermolecular force, which varies with molecular separation r according to F=μr−n where n is a number and μ is a constant. If η is a function of the mass m of the molecules, their mean speed v, and the constant μ than which of the following is correct-
η∝mn+1vn+3μn−2
η∝mn+1n−1vn+3n−1μ−2n−1
η∝mnv−nμ−2
η∝mvμ−n
The correct Answer is:B
To solve the problem regarding the viscosity η of a gas and its dependence on mass m, mean speed v, and a constant μ, we will perform dimensional analysis. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the relationship
The viscosity η is said to depend on the mass m of the molecules, their mean speed v, and a constant μ. We can express this relationship as:
η=k⋅ma⋅vb⋅μc
where k is a proportionality constant and a,b,c are the powers we need to determine.
Step 2: Determine the dimensions of viscosity
Viscosity η can be defined through the formula for viscous force:
F=6πηrv
From this, we can rearrange to find η:
η=F6πrv
The dimensions of force F are:
(F)=MLT−2
The dimensions of radius r are:
(r)=L
The dimensions of speed v are:
(v)=LT−1
Substituting these into the viscosity formula gives:
(η)=MLT−2L⋅LT−1=MLT−2L2T−1=ML−1T−1
Step 3: Write down the dimensions of the variables
Now we have:
- (m)=M
- (v)=LT−1
- (μ) needs to be determined from the force equation F=μr−n.
Step 4: Determine the dimensions of μ
From the equation F=μr−n, we can express μ as:
μ=Fr−n=F⋅rn
Thus, the dimensions of μ are:
(μ)=(F)⋅(r)n=(MLT−2)⋅(L)n=MLn+1T−2
Step 5: Substitute dimensions into the equation
Now substituting the dimensions into the equation for η:
(ML−1T−1)=(M)a⋅(LT−1)b⋅(MLn+1T−2)c
This expands to:
M1L−1T−1=Ma⋅Lb+c(n+1)⋅T−b−2c
Step 6: Equate the powers of dimensions
Equating the powers of M, L, and T:
1. For M: 1=a+c
2. For L: −1=b+c(n+1)
3. For T: −1=−b−2c
Step 7: Solve the equations
From the first equation:
c=1−a
Substituting c into the second and third equations:
- Second equation:
−1=b+(1−a)(n+1)⟹−1=b+n+1−a(n+1)⟹b=−n−a(n+1)
- Third equation:
−1=−b−2(1−a)⟹−1=−b−2+2a⟹b=1+2a
Step 8: Substitute and solve for a
Setting the two expressions for b equal:
−n−a(n+1)=1+2a
Rearranging gives:
−n−1=a(n+1+2)⟹a=−n−1n+3
Step 9: Find b and c
Substituting a back into the equations will yield b and c.
Final Result
After solving for a,b,c, we can express η in terms of m,v,μ as:
η∝m−n−1n+3vn+3n+1μ−2n+1
Conclusion
The correct option will be the one that matches this derived relationship.
The viscosity η is said to depend on the mass m of the molecules, their mean speed v, and a constant μ. We can express this relationship as:
η=k⋅ma⋅vb⋅μc
where k is a proportionality constant and a,b,c are the powers we need to determine.
Viscosity η can be defined through the formula for viscous force:
F=6πηrv
From this, we can rearrange to find η:
η=F6πrv
The dimensions of force F are:
(F)=MLT−2
The dimensions of radius r are:
(r)=L
The dimensions of speed v are:
(v)=LT−1
Substituting these into the viscosity formula gives:
(η)=MLT−2L⋅LT−1=MLT−2L2T−1=ML−1T−1
Now we have:
- (m)=M
- (v)=LT−1
- (μ) needs to be determined from the force equation F=μr−n.
From the equation F=μr−n, we can express μ as:
μ=Fr−n=F⋅rn
Thus, the dimensions of μ are:
(μ)=(F)⋅(r)n=(MLT−2)⋅(L)n=MLn+1T−2
Now substituting the dimensions into the equation for η:
(ML−1T−1)=(M)a⋅(LT−1)b⋅(MLn+1T−2)c
This expands to:
M1L−1T−1=Ma⋅Lb+c(n+1)⋅T−b−2c
Equating the powers of M, L, and T:
1. For M: 1=a+c
2. For L: −1=b+c(n+1)
3. For T: −1=−b−2c
From the first equation:
c=1−a
Substituting c into the second and third equations:
- Second equation:
−1=b+(1−a)(n+1)⟹−1=b+n+1−a(n+1)⟹b=−n−a(n+1)
- Third equation:
−1=−b−2(1−a)⟹−1=−b−2+2a⟹b=1+2a
Setting the two expressions for b equal:
−n−a(n+1)=1+2a
Rearranging gives:
−n−1=a(n+1+2)⟹a=−n−1n+3
Substituting a back into the equations will yield b and c.
After solving for a,b,c, we can express η in terms of m,v,μ as:
η∝m−n−1n+3vn+3n+1μ−2n+1
The correct option will be the one that matches this derived relationship.
Topper's Solved these Questions
Similar Questions
The word fluid means a substance having particles which readily of its magnitude (a small shear stress, which may appear to be of negligible will cause deformation in the fluid). Fluids are charactrised by such properties as density. Specific weight, specific gravity, viscosity etc. Density of a substance is defined as mass per unit volume and it is denoted by. The specific gravity represents a numerical ratio of two densities, and water is commonly taken as a reference substance. Specific gravity of a substance in written as the ratio of density of substance to the density of water. Specific weight represents the force exerted by gravity on a unit volume of fluid. It is related to the density as the product of density of a fluid and acceleration due to gravity. Viscosity is the most important and is recognized as the only single property which influences the fluid motion to a great extent. The viscosity is the property by virtue of which a fluid offers resistance to deformation under the influenece if shear force. The force between the layers opposing relative motion between them are known as forces of viscosity. When a boat moves slowly on the river remains at rest. Velocities of different layers are different. Let v be the velocity of the level at a distance y from the bed and V+dv be the velocity at a distance y+dy. The velocity differs by dv in going through a distance by perpendicular to it. The quantity dvdy is called velocity gradient. The force of viscosity between two layers of a fluid is proportional to velocity gradient and Area of the layer.
F∝A & F∝dvdy
F=−ηAdvdy (−ve sign shown the force is frictional in nature and opposes relative motion. η coefficient of dynamic viscosity
Shear stress FA=−ηdvdy
and simultaneously kinematic viscosity is defined as the dynamic viscosity divided by the density. If is denoted as v. The viscosity of a fluid depends upon its intermolecular structure. In gases, the molecules are widely spaced resulting in a negligible intermolecular cohesion, while in liquids the molecules being very close to each other, the cohesion is much larger with the increases of temperature, the cohesive force decreases rapidly resulting in the decreases of viscosity. In case of gases, the viscosity is mainly due to transfer of molecular momentum in the transerve direction brought about by the molecular agitation. Molecular agitation increases with rise in temperature. Thus we conclude that viscosity of a fluid may thus be considered to be composed of two parts, first due to intermolecuar cohesion and second due to transfer of molecular momentum.
If the velocity profile is given by
v=23y−y2v is velocity in m/secy is in meter above the bad. Determine shear stress at y=0.15m, & η=0.863Ns/m2
View SolutionThe word fluid means a substance having particles which readily of its magnitude (a small shear stress, which may appear to be of negligible will cause deformation in the fluid). Fluids are charactrised by such properties as density. Specific weight, specific gravity, viscosity etc. Density of a substance is defined as mass per unit volume and it is denoted by. The specific gravity represents a numerical ratio of two densities, and water is commonly taken as a reference substance. Specific gravity of a substance in written as the ratio of density of substance to the density of water. Specific weight represents the force exerted by gravity on a unit volume of fluid. It is related to the density as the product of density of a fluid and acceleration due to gravity. Viscosity is the most important and is recognized as the only single property which influences the fluid motion to a great extent. The viscosity is the property by virtue of which a fluid offers resistance to deformation under the influenece if shear force. The force between the layers opposing relative motion between them are known as forces of viscosity. When a boat moves slowly on the river remains at rest. Velocities of different layers are different. Let v be the velocity of the level at a distance y from the bed and V+dv be the velocity at a distance y+dy. The velocity differs by dv in going through a distance by perpendicular to it. The quantity dvdy is called velocity gradient. The force of viscosity between two layers of a fluid is proportional to velocity gradient and Area of the layer.
F∝A & F∝dvdy
F=−ηAdvdy (−ve sign shown the force is frictional in nature and opposes relative motion. η coefficient of dynamic viscosity
Shear stress FA=−ηdvdy
and simultaneously kinematic viscosity is defined as the dynamic viscosity divided by the density. If is denoted as v. The viscosity of a fluid depends upon its intermolecular structure. In gases, the molecules are widely spaced resulting in a negligible intermolecular cohesion, while in liquids the molecules being very close to each other, the cohesion is much larger with the increases of temperature, the cohesive force decreases rapidly resulting in the decreases of viscosity. In case of gases, the viscosity is mainly due to transfer of molecular momentum in the transerve direction brought about by the molecular agitation. Molecular agitation increases with rise in temperature. Thus we conclude that viscosity of a fluid may thus be considered to be composed of two parts, first due to intermolecuar cohesion and second due to transfer of molecular momentum.
Viscosity of liquids
View Solution
Knowledge Check
which of the following expressions is correct (n= number of moles of the gas, NA= Avogadro constant, m = mass of 1 molecule of the gas, N = number of molecules of the gas)?
An=mNABm=NACN=nNADm=n/NAWhich of the following expressions is correct ( n=no. of moles of the gas, NA= Avogadro constant m=mass of 1 molecule of the gas, N = no of molecules of the gas) ? .
An=mNABm=NACN=nNADm=n/NAA flat plate is moving normal to its plane through a gas under the action of a constant force F. The gas is kept at a very low pressure. The speed of the plate v is much less than the average speed u of the gas molecules. Which of the following options is/are true?
AThe pressure difference between the leading and trailing faces of the plate is proportional to uvBAt a later time the external force F balances the resistive forceCThe resistive force experienced by the plate is proportional to vDThe plate will continue to move with constant non-zero acceleration, at all times
A particle of mass m moves along a circle of radius R with a normal acceleration varying with time as aN=kt2 where k is a constant. Find the time dependence of power developed by all the forces acting on the particle and the mean value of this power averaged over the first t seconds after the beginning of the motion.
View SolutionIn the following problems, indicate the correct direction of friction force acting on the cylinder, which is pulled on a rough surface by a constant force F.
A cylinder of mass M and radius R is pulled horizontally by a force F. The friction force can be given by which of the following diagrams.
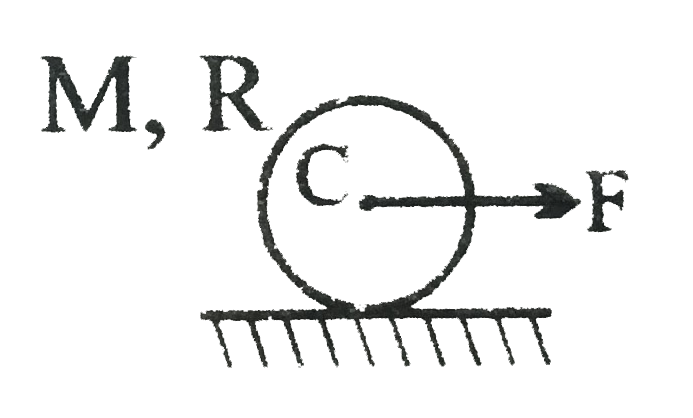 .
.
View SolutionA body of mass 'm' is moving with constant speed v on a track shown in figure. At point A and point B radius of curvature is R. NA,NB and NC represents normal reactions at A, B and C which of the following option is correct ?
View SolutionA body of mass 'm' is moving with constant speed v on a track shown in figure. At point A and point B radius of curvature is R. NA,NB and NC represents normal reactions at A, B and C which of the following option is correct ?
View SolutionSuppose an electron is attracted toward the origin by a forcekr where k is a constant and r is the distance of the electron from the origein .By appling Bohr model to this system the radius of the nth orbital of the electron is found to be rn and the kinetic energy of the electron to be Tn , Then which of the following is true ?
View Solution