The length of the potentiometer wire is 600 cm and a current of 40 mA is flowing in it. When a cell of emf 2 V and internal resistance 10Ω is balanced on this potentiometer the balance length is found to be 500 cm. The resistance of potentiometer wire will be
20Ω
40Ω
60Ω
80Ω
The correct Answer is:C
To find the resistance of the potentiometer wire, we can follow these steps:
Step 1: Understand the relationship between EMF, potential gradient, and balance length
The EMF (E) of the cell is related to the potential gradient (V/L) and the balance length (L0) by the formula:
E=(VL)×L0
Where:
- E = EMF of the cell (2 V)
- V = potential difference across the potentiometer wire
- L = total length of the potentiometer wire (600 cm)
- L0 = balance length (500 cm)
Step 2: Calculate the potential gradient
The potential gradient (V/L) can be expressed in terms of the current (I) flowing through the potentiometer wire and its resistance (R):
V=I×R
Thus, we can rewrite the potential gradient as:
VL=I×RL
Step 3: Substitute the values into the equation
Substituting the expression for V into the EMF equation:
E=(I×RL)×L0
Now substituting the known values:
- E=2V
- I=40mA=40×10−3A
- L=600cm=600×10−2m
- L0=500cm=500×10−2m
Step 4: Rearranging the equation to find R
Now we can rearrange the equation to solve for R:
2=(40×10−3×R600×10−2)×(500×10−2)
Step 5: Simplifying the equation
Rearranging gives:
2=40×10−3×R×500×10−2600×10−2
2=40×500×R600×10−3
2=20000×R600×10−3
2=20000600×R×10−3
Step 6: Solving for R
Now we can solve for R:
R=2×60020000×10−3
R=120020
R=60Ω
Thus, the resistance of the potentiometer wire is 60 ohms.
The EMF (E) of the cell is related to the potential gradient (V/L) and the balance length (L0) by the formula:
E=(VL)×L0
Where:
- E = EMF of the cell (2 V)
- V = potential difference across the potentiometer wire
- L = total length of the potentiometer wire (600 cm)
- L0 = balance length (500 cm)
The potential gradient (V/L) can be expressed in terms of the current (I) flowing through the potentiometer wire and its resistance (R):
V=I×R
Thus, we can rewrite the potential gradient as:
VL=I×RL
Substituting the expression for V into the EMF equation:
E=(I×RL)×L0
Now substituting the known values:
- E=2V
- I=40mA=40×10−3A
- L=600cm=600×10−2m
- L0=500cm=500×10−2m
Now we can rearrange the equation to solve for R:
2=(40×10−3×R600×10−2)×(500×10−2)
Rearranging gives:
2=40×10−3×R×500×10−2600×10−2
2=40×500×R600×10−3
2=20000×R600×10−3
2=20000600×R×10−3
Now we can solve for R:
R=2×60020000×10−3
R=120020
R=60Ω
Topper's Solved these Questions
Similar Questions
In a potentiometer circuit, the emf of driver cell is 2V and internal resistance is 0.5Ω. The potentiometer wire is 1m long . It is found that a cell of emf 1V and internal resistance 0.5Ω is balanced against 60 cm length of the wire. Calculate the resistance of potentiometer wire.
View SolutionA battery of e.m.f. 10 V and internal resistance 2Ω is connected in primary circuit with a uniform potentiometer wire and a rheostat whose resistance is fixed at 998Ω.A battery of unknown e.m.f. is being balanced on this potentiometer wire and balancing length is found to be 50 cm.When area of cross section of potentiometer wire is doubled, then balancing length is found to be 75 cm.
(i)Calculate e.m.f. of the battery.
(ii)Calculate resistivity of potentiometer wire if length of wire is 100 cm and area of cross-section (initially) is 100cm2.
View Solution
Knowledge Check
There is a potentiometer wire of length 1200 cm and 60 mA current is flowing in it. A battery of emf 5V and internal resistance of 20ohm is balanced on potentiometer wire with balancing length 1000 cm. The resistance of potentiometer wire is
A80ohmB100ohmC120ohmD60ohmThe potentiometer wire is of length 1200 cam and it carries a current of 60 mA. For a cell of emf 5V and internal resistance of 20Ω, the null point of it is found to be at 1000 cm.The resistance of potentiometer wire is
A60ΩB120ΩC100ΩD80ΩThe length of a potentiometer wire AB is 600cm, and it carries a constant current of 40mA from A to B. For a cell of emf 2V and internal resistance 10Ω, the null point is found at 500cm from A. When a voltmeter is connected across the cell, the balancing length of the wire is decreased by 10cm.
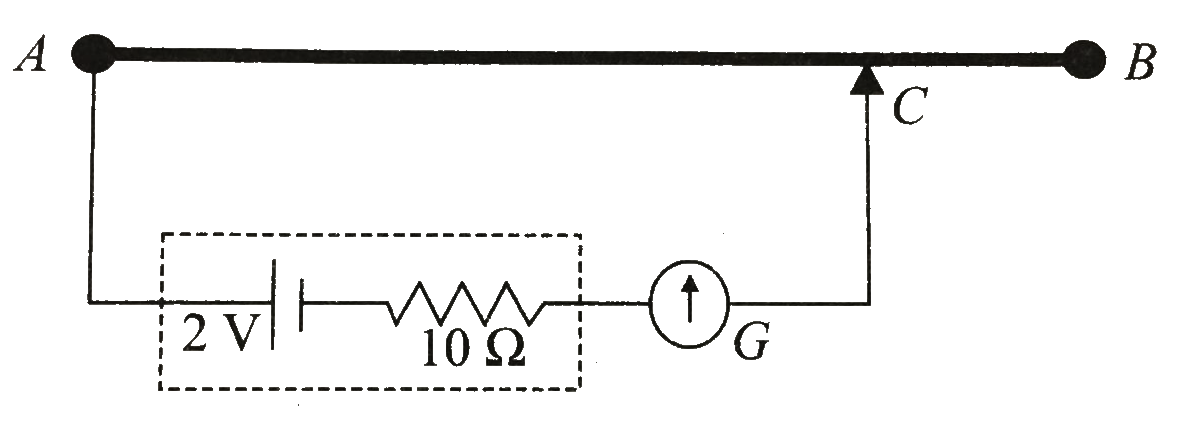
Reading of the voltmeter isA2VB2.04VC1.96VD1.0V
The length of a potentiometer wire AB is 600cm, and it carries a constant current of 40mA from A to B. For a cell of emf 2V and internal resistance 10Ω, the null point is found at 500cm from A. When a voltmeter is connected across the cell, the balancing length of the wire is decreased by 10cm.
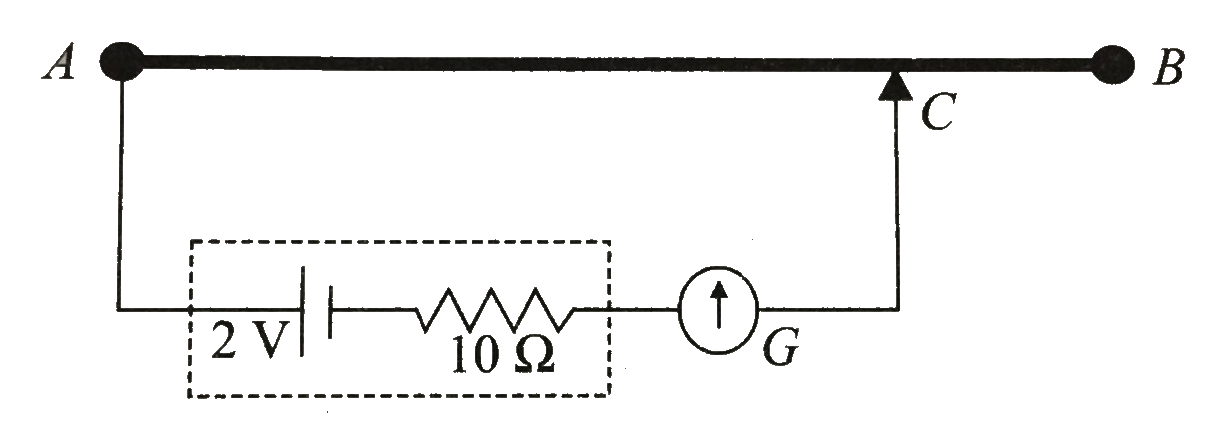
Potential gradient along AB is
View SolutionThe length of a potentiometer wire is 600 cm and it carries a current of 40mA. For a cell of emf 2V and internal resistance 10Ω, the null point is found to be at 500cm. On connecting a voltmeter acros the cell, the balancing length is decreased by 10cm
The resistance of the voltmeter is
View SolutionThe length of a potentiometer wire is 600cm and it carries a current of 40mA. For a cell of emf 2V and internal resistance 10Ω, the null point is found to be at 500cm. On connecting a voltmeter across the cell, the balancing length is decreased by 10cm
The voltmeter reading will be
View SolutionThe wire of potentiometer has resistance 4Ω and length 1m. It is connected to a cell of e.m.f. 2V and internal resistance 1Ω. The current flowing through the potentiometer wire is
View SolutionThe wire of potentiometer has resistance 4Ω and length Im. It is connected to a cell of EMF 2V and internal resistance1Ω. Ifa cell ofEMF 1.2V is balanced byit, the balancing length will be:
View Solution
