(dGdp)T=
V
S
−S
−V
The correct Answer is:A
To solve the question (dGdp)T, we need to understand the relationship between Gibbs free energy (G), pressure (p), and temperature (T). Let's break it down step by step.
Step 1: Understand Gibbs Free Energy
Gibbs free energy is defined by the equation:
G=H−TS
where H is enthalpy, T is temperature, and S is entropy.
Step 2: Differentiate Gibbs Free Energy
To find (dGdp)T, we need to differentiate G with respect to pressure p while keeping temperature T constant. We can express the differential of G as:
dG=dH−TdS−SdT
Since we are keeping T constant, dT=0, so the equation simplifies to:
dG=dH−TdS
Step 3: Use the Enthalpy Relation
Enthalpy H can be expressed in terms of internal energy U and pressure-volume work:
H=U+pV
Differentiating H gives:
dH=dU+pdV+Vdp
Step 4: Substitute into the Differential
Now substituting dH into the equation for dG:
dG=(dU+pdV+Vdp)−TdS
This can be rearranged to:
dG=dU+pdV+Vdp−TdS
Step 5: Express Internal Energy Differential
Using the first law of thermodynamics, we know that:
dU=TdS−pdV
Substituting this into the equation for dG:
dG=(TdS−pdV)+pdV+Vdp−TdS
This simplifies to:
dG=Vdp
Step 6: Take the Derivative
Now, taking the derivative of G with respect to p at constant T:
(dGdp)T=V
Conclusion
Thus, the value of (dGdp)T is equal to the volume V.
Final Answer
(dGdp)T=V
Gibbs free energy is defined by the equation:
G=H−TS
where H is enthalpy, T is temperature, and S is entropy.
To find (dGdp)T, we need to differentiate G with respect to pressure p while keeping temperature T constant. We can express the differential of G as:
dG=dH−TdS−SdT
Since we are keeping T constant, dT=0, so the equation simplifies to:
dG=dH−TdS
Enthalpy H can be expressed in terms of internal energy U and pressure-volume work:
H=U+pV
Differentiating H gives:
dH=dU+pdV+Vdp
Now substituting dH into the equation for dG:
dG=(dU+pdV+Vdp)−TdS
This can be rearranged to:
dG=dU+pdV+Vdp−TdS
Using the first law of thermodynamics, we know that:
dU=TdS−pdV
Substituting this into the equation for dG:
dG=(TdS−pdV)+pdV+Vdp−TdS
This simplifies to:
dG=Vdp
Now, taking the derivative of G with respect to p at constant T:
(dGdp)T=V
Thus, the value of (dGdp)T is equal to the volume V.
(dGdp)T=V
Topper's Solved these Questions
Similar Questions
Let the population of rabbits surviving at a time t be governed by the differential equation (dptdt=12p(t)−200. If p(0)=100 , then p(t) equals
View SolutionThe population p(t) at time t of a certain mouse species satisfies the differential equation (dptdt=0.5p(t)−450 If p(0)=850 , then the time at which the population becomes zero is (1) 2 ln 18 (2) ln 9 (3) 12 In 18 (4) ln 18
View Solution
Knowledge Check
which of the following graphs correctly represents the vatiation β=−(dVdP)T/V with P for an ideal gas at constant temperature ? .
A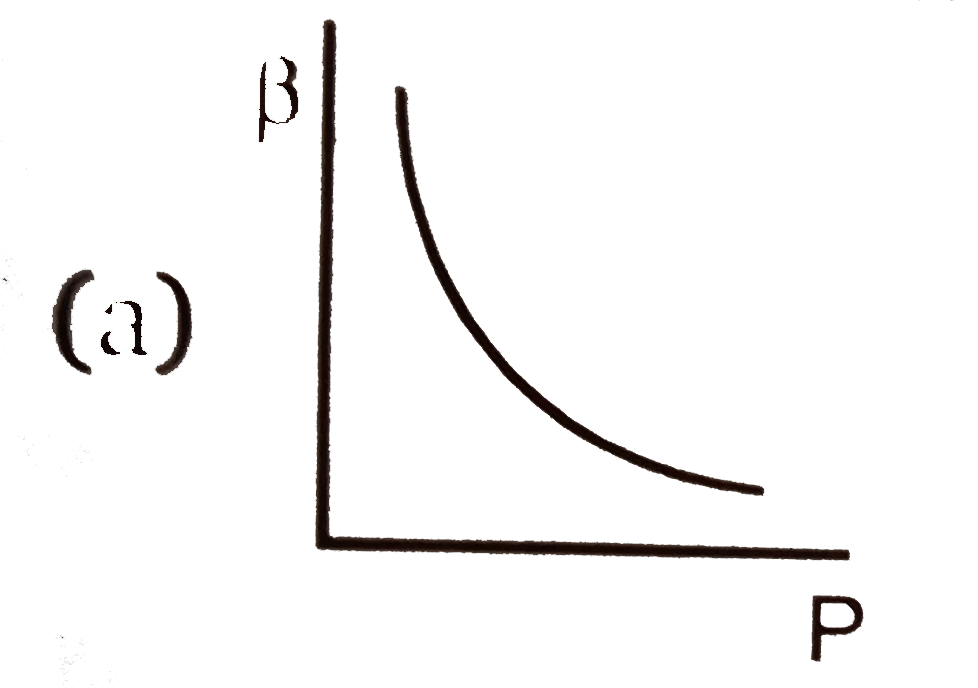 B
B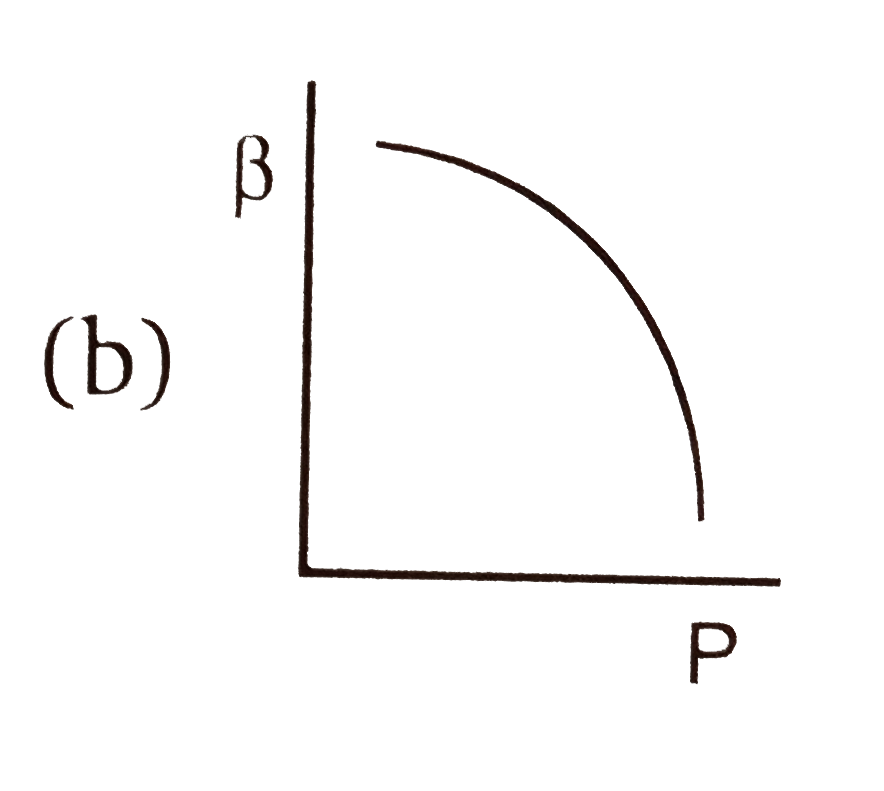 C
C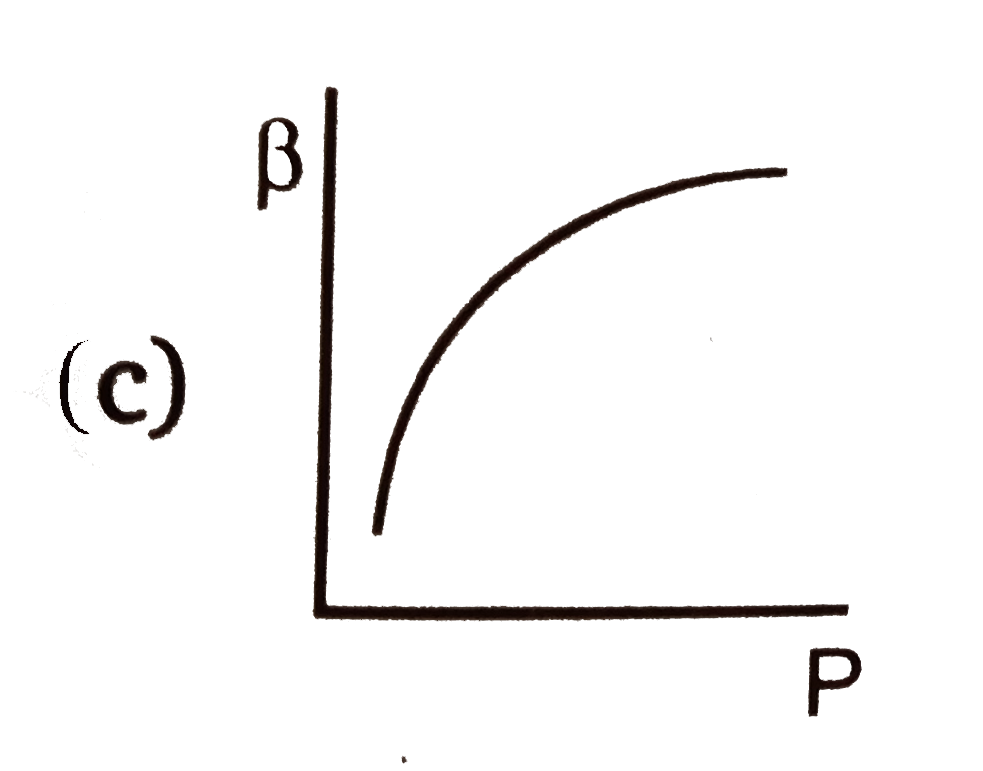 D
D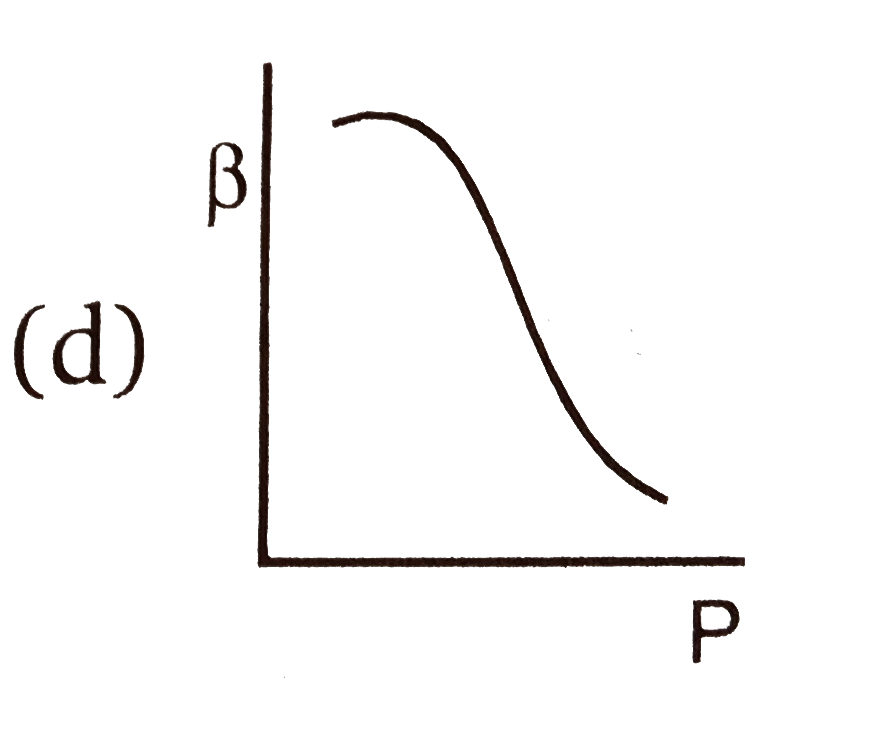
निम्न में से कौनसा आरेख स्थिर ताप पर एक आदर्श गैस के लिए β[β=−dV(dP)T/V] , P के मध्य सही परिवर्तन को प्रदर्शित करता है?
A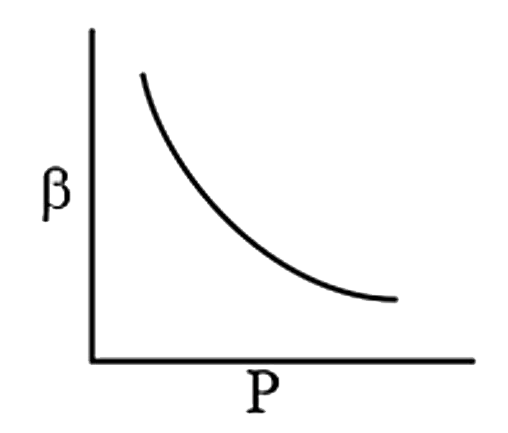 B
B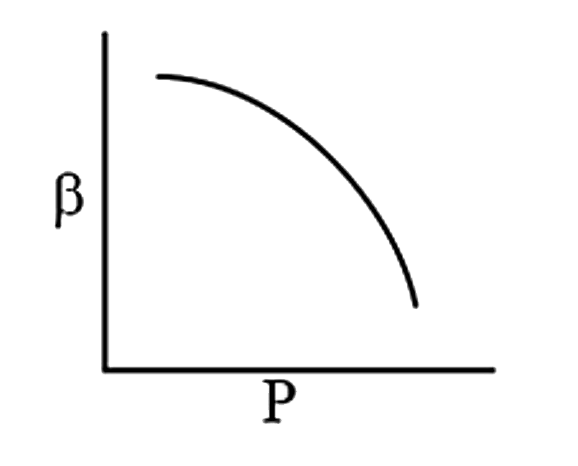 C
C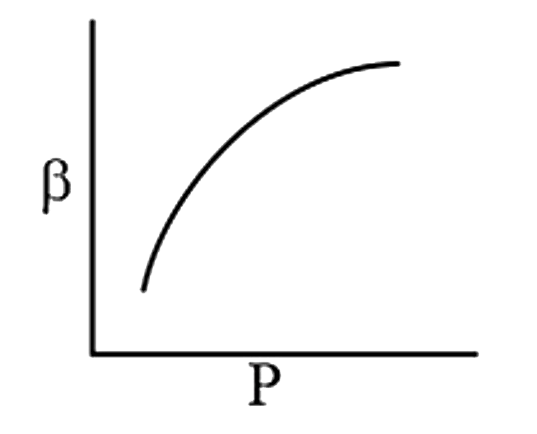 D
D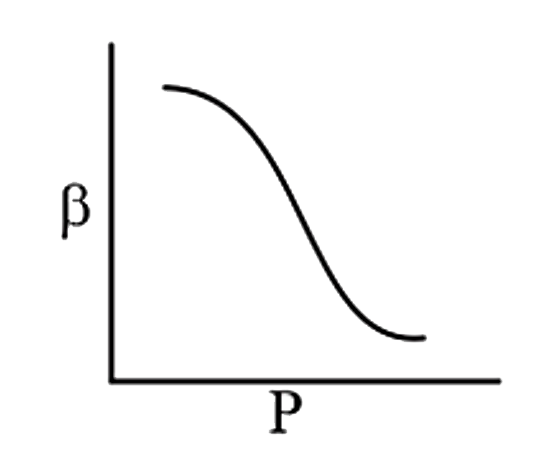
Which of following graphs correctly represent variation of α=−(dV/dP)TV with P for fixed amount of an ideal gas at constant temperature ?
A B
B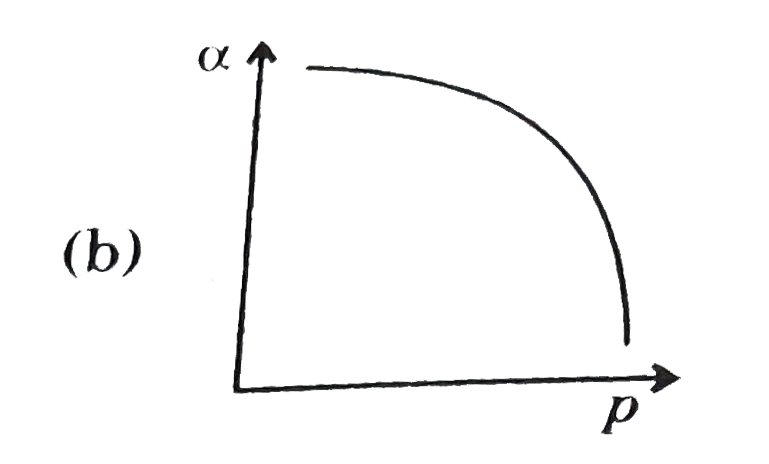 C
C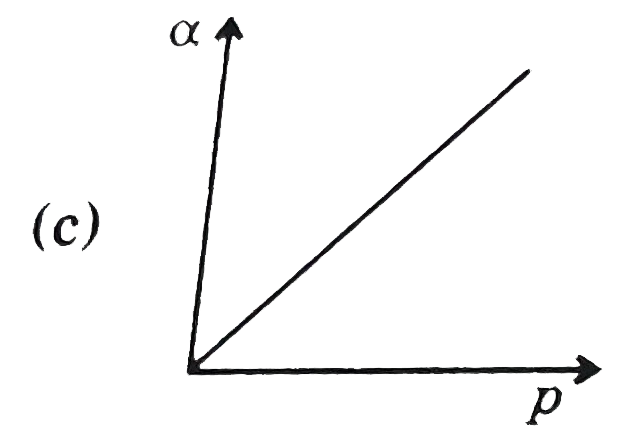 D
D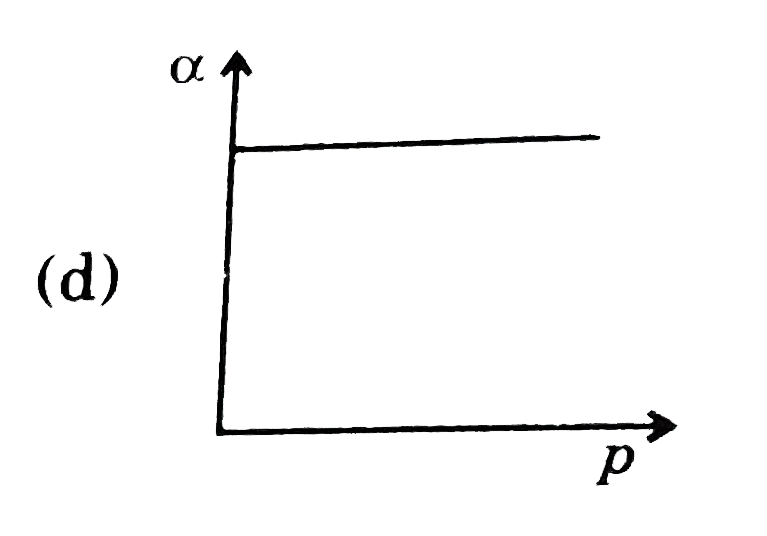
Let the population of rabbits surviving at a time t be governed by the differential equation dp(t)dt=12p(t)−200. If p(0)=100, then p(t) equals
View SolutionThe population p(t) at time t of a certain mouse species follows the differential equation dp(t)dt=0.5 p(t)-450. If p(0)=850, then the time at which the population becomes zero is
View SolutionLet the population of rabbits surviving at a time t be governed by the differential equation (dptdt=12p(t)−200. If p(0)=100 , then p(t) equals (1) 400−300et/2 (2) 300−200e−t/2 (3) 600−500et/2 (4) 400−300e−t/2
View SolutionThe population p(t) at a time t of a certain mouse species satisfies the differential equation dp(t)dt=0.5p(t)−450. If p(0)=850. Then the time at which the population becomes zero is
View SolutionIf pv=81, then dpdv at v=9 is equal to
View Solution
