A ball is dropped from a height h on a floor. The coefficient of restitution for the collision between the ball and the floor is e. The total distance covered by the ball before it comes to the rest.
h(1−2e2)
h[1+e21−e2]
h[1−e21+e2]
he2
The correct Answer is:B
To solve the problem of finding the total distance covered by a ball dropped from a height h before it comes to rest, given the coefficient of restitution e, we can break down the solution into several steps.
1. Initial Drop:
The ball is dropped from a height h. When it hits the ground, it will have a velocity v just before the impact. Using the equation of motion:
v2=u2+2gh
where u=0 (initial velocity), we find:
v2=2gh⇒v=√2gh
2. Velocity After Collision:
After the collision, the velocity of the ball just after it rebounds is given by the coefficient of restitution:
u=e⋅v=e⋅√2gh
3. Height After First Bounce:
The ball will rise to a height h′ after the first bounce. Using the equation of motion again:
0=u2−2gh′⇒h′=u22g=(e⋅√2gh)22g=e2⋅2gh2g=e2h
4. Subsequent Bounces:
After the first bounce, the ball will continue to bounce and rise to heights that are reduced by the factor of e2 for each subsequent bounce. The heights after each bounce can be expressed as:
- First bounce height: h′=e2h
- Second bounce height: h′′=e4h
- Third bounce height: h′′′=e6h
- And so on...
5. Total Distance Calculation:
The total distance D covered by the ball includes the initial drop and the distances covered during the upward and downward motions for each bounce:
D=h+2(h′+h′′+h′′′)+…
This can be expressed as:
D=h+2(e2h+e4h+e6h+…)
6. Sum of Infinite Geometric Series:
The series e2h+e4h+e6h+… is a geometric series with the first term a=e2h and common ratio r=e2:
Sum=a1−r=e2h1−e2
Therefore, the total distance becomes:
D=h+2⋅e2h1−e2=h+2e2h1−e2
7. Final Expression:
Combining the terms, we can express the total distance covered by the ball before it comes to rest as:
D=h(1+2e21−e2)=h(1−e2+2e21−e2)=h(1+e21−e2)
Final Answer:
D=h(1+e21−e2)
The ball is dropped from a height h. When it hits the ground, it will have a velocity v just before the impact. Using the equation of motion:
v2=u2+2gh
where u=0 (initial velocity), we find:
v2=2gh⇒v=√2gh
After the collision, the velocity of the ball just after it rebounds is given by the coefficient of restitution:
u=e⋅v=e⋅√2gh
The ball will rise to a height h′ after the first bounce. Using the equation of motion again:
0=u2−2gh′⇒h′=u22g=(e⋅√2gh)22g=e2⋅2gh2g=e2h
After the first bounce, the ball will continue to bounce and rise to heights that are reduced by the factor of e2 for each subsequent bounce. The heights after each bounce can be expressed as:
- First bounce height: h′=e2h
- Second bounce height: h′′=e4h
- Third bounce height: h′′′=e6h
- And so on...
The total distance D covered by the ball includes the initial drop and the distances covered during the upward and downward motions for each bounce:
D=h+2(h′+h′′+h′′′)+…
This can be expressed as:
D=h+2(e2h+e4h+e6h+…)
The series e2h+e4h+e6h+… is a geometric series with the first term a=e2h and common ratio r=e2:
Sum=a1−r=e2h1−e2
Therefore, the total distance becomes:
D=h+2⋅e2h1−e2=h+2e2h1−e2
Combining the terms, we can express the total distance covered by the ball before it comes to rest as:
D=h(1+2e21−e2)=h(1−e2+2e21−e2)=h(1+e21−e2)
D=h(1+e21−e2)
Topper's Solved these Questions
Similar Questions
A ball is dropped from a height h on to a floor . If the cofficient of restitution is e, calculate the height the ball first rebounds ?
View SolutionA spherical ball falls from a height h on to a floor of coefficient of restitution e . Calculate the total distance described by the ball before it comes to rest .
View Solution
Knowledge Check
A ball is dropped from a height h onto a floor and rebounds to a height h/6. The coefficient of restitution between the ball and the floor is
A12B14C23D1√6A ball is dropped from a certain height on a horizontal floor. The coefficient of restitution between the ball and the floor is 12. The displacement time graph of the ball will be.
A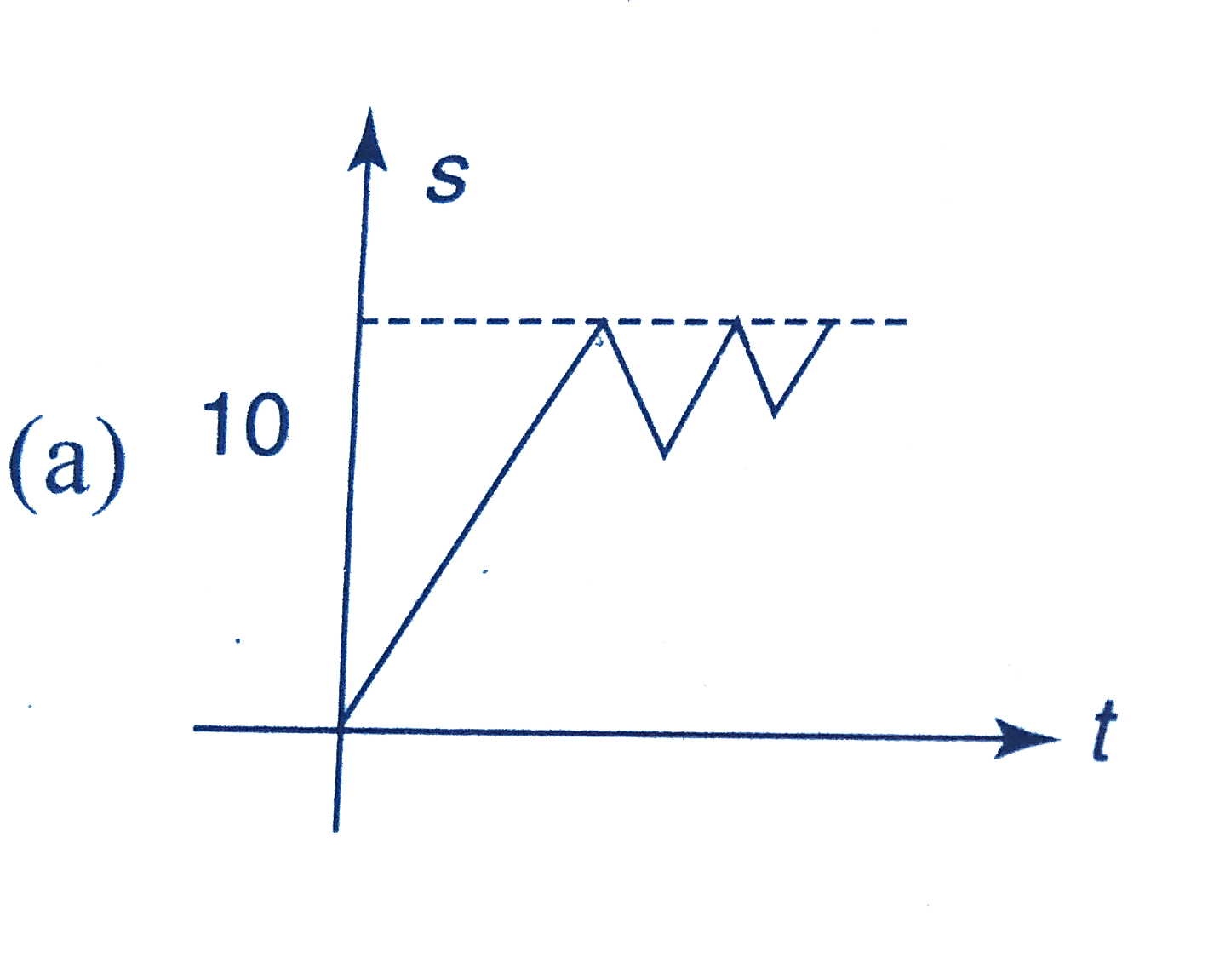 .B
.B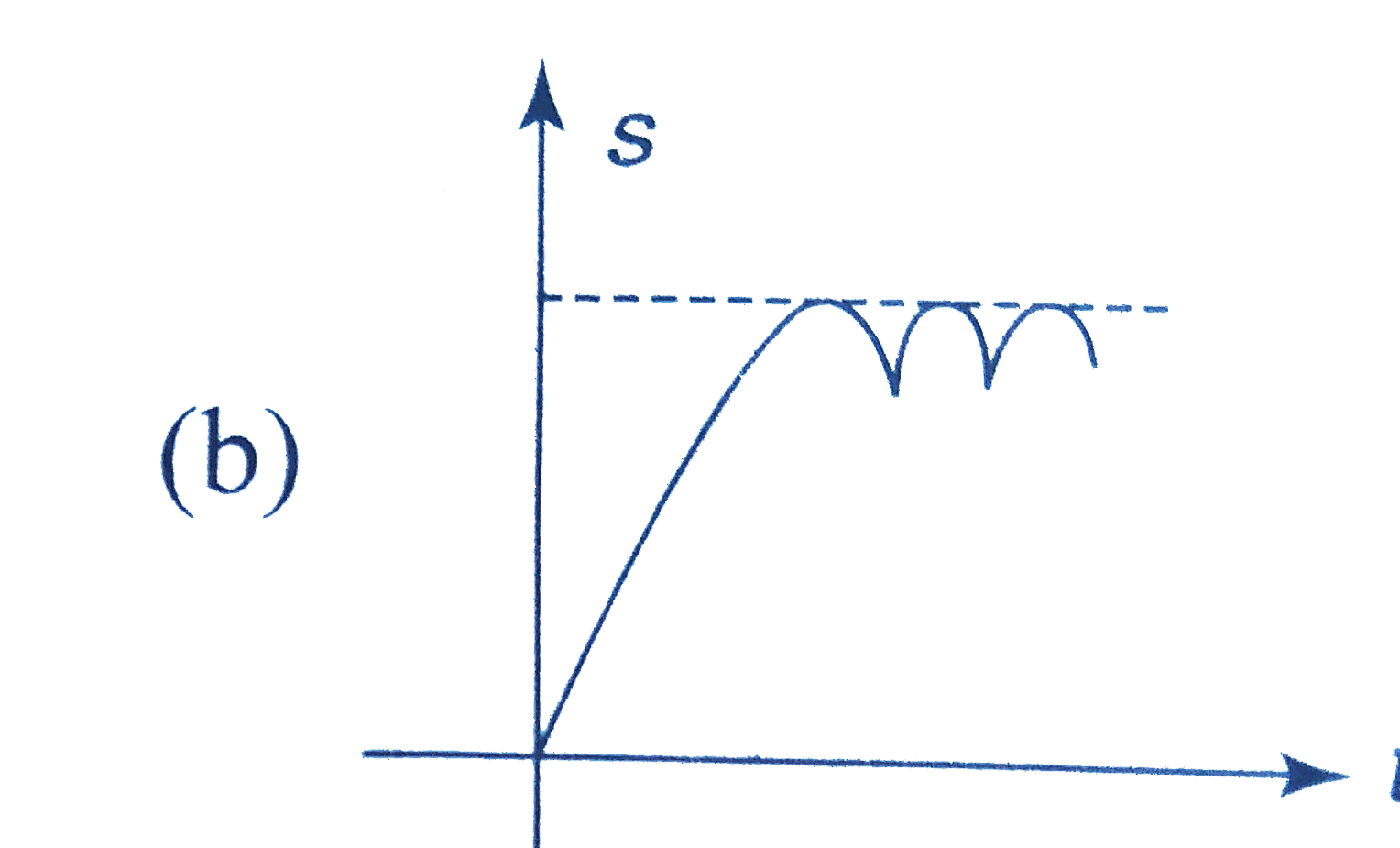 .C
.C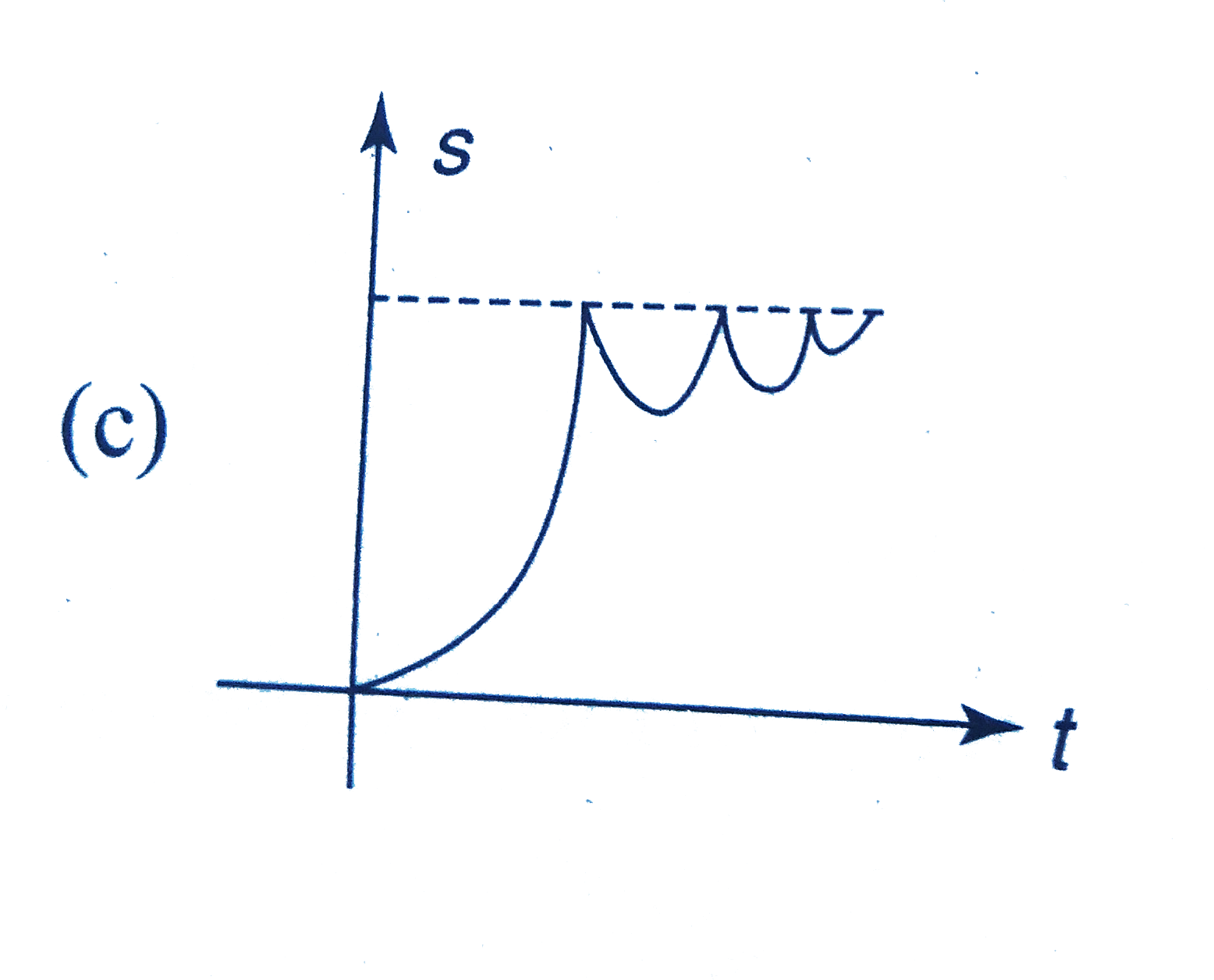 .D
.D .
.A ball is dropped from a height 'h' on to a floor of coefficient of restitution 'e'. The total distance covered by the ball just before second hit is
Ah(1−2e2)Bh(1+2e2)Ch(1+e2)Dhe2
A ball is dropped from a height of 3m. If coefficient of restitution between the surface and ball is 0.5, then the total distance covered by the before it comes to rest is
View SolutionA ball falls from rest from a height h onto a floor, and rebounds to a height h/4. The coefficient of restitution between the ball and the floor is
View SolutionA ball is dropped from a height h on to a floor . If the cofficient of restitution is e, calculate the height the ball first rebounds ?
View SolutionA ball is dropped from height 'H' onto a horizontal surface. If the coefficient of restitution is 'e' then the total time after which it comes to rest is
View SolutionA ball is dropped from a height h . If the coefficient of restitution be e , then to what height will it rise after jumping twice from the ground
View Solution
