Two particles A and B located at points (0,−10√3) and (0,0) in xy plane. They start moving simultaneously at time t=0 with constant velocities →VA=5ˆim/s and →VB=−5√3ˆjm/s, respectively. Time when they are closest to each other is found to be K/2 second. Find K. All distance are given in meter.
The correct Answer is:3
Step by step video, text & image solution for Two particles A and B located at points (0,-10sqrt(3)) and (0,0) in xy plane. They start moving simultaneously at time t=0 with constant velocities vecV_(A)=5hatim//s and vecV_(B)=-5sqrt(3)hatjm//s, respectively. Time when they are closest to each other is found to be K//2 second. Find K. All distance are given in meter. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Two particles are located on a horizontal plane at a distance 60m. At t=0 both the particles are simultaneously projected at angle 45∘ with velocities 2ms−1and14ms−1, respectively. Find
(a) Minimum separation between them during motion.
(b) At what time is the separation between them minimum ?
 .
.
View SolutionVelocity and acceleration of a particle at time t=0are u=(2ˆi+3ˆj)m/sanda=(4ˆi+3ˆj)m/s2 respectively. Find the velocity and displacement if particle at t=2s.
View Solution
Knowledge Check
Two particles A and B are located in x−y plane at points (0,0) and (0,4m). They simultaneoulsy start moving with velocities vA=2ˆjm/s and vB=2ˆim/s. Select the correct alternative(s)
Athe distance between them is constantBThe distance between them first decreases and then increasesCthe shortest distance between them is 2√2mDTime after which they are at minimum distances is 1sTwo particles are initially located at points A and B distant d apart. They start moving at time t=0 such that the velocity →u of B is always along the horizontal and velocity →v of A is contiunously aimed at B. At t=0,→u is perpendicu lar to →v The particles will meet after time:
Avdv2−u2Bv2+u2udCv2−u2vdDud(v2−u2)Two particles start moving simultaneously from points (0, 0) and (1, 0) respectively in the OXY plane with uniform velocities v1 and v2 as shown in the figure. It is found that they collide. Then
 Av1=v2√2Bv1=v2Cv2=√2v1Dv2=v1√32
Av1=v2√2Bv1=v2Cv2=√2v1Dv2=v1√32
Two particles A and B separated by 10 m at time t=0 are moving uniformly. A is moving along line AB at a constant velocity of 4m/s and B is moving perpendicular to the velocity of A at a constant velocity of 5m/s. After what time the two particles will be nearest to each other?

View SolutionTwo particles of masses 1kg and 2kg respectively are initially 10m aprt. At time t=0, they start moving towards each other with uniform speeds 2m/s and 1m/s respectively. Find the displacement of their centre of mass at t=1s.
View SolutionFrom the origin, a particle starts at t = 0 s with a velocity →v=7.0ˆim/s and moves in the xy plane with a constant acceleration of →a=(−9.0ˆi+3.0ˆj)m/s2. At the time the particle reaches the maximum x coordinate, what is its (a) velocity and (b) position vector?
View SolutionTwo particles A and B are moving with constant velocities V1=ˆj and v2=2ˆi respectively in XY plane. At time t=0, the particle A is at co-ordinates (0,0) and B is at (-4,0). The angular velocities of B with respect to A at t=2s is (all physical quantities are in SI units)
View SolutionTwo particles A and B are located at point (0m,50m) at t=0. The particle A moves withy a constant velocity and the particle B moves on a circle of radius 50 m having centre at origin (0,0) as shown in figure. The pasrticle B has a constant speed 5πm/s. What will be the velocity of particle A so that both the pasrticles reach at point (50m,0m) simultaneously.
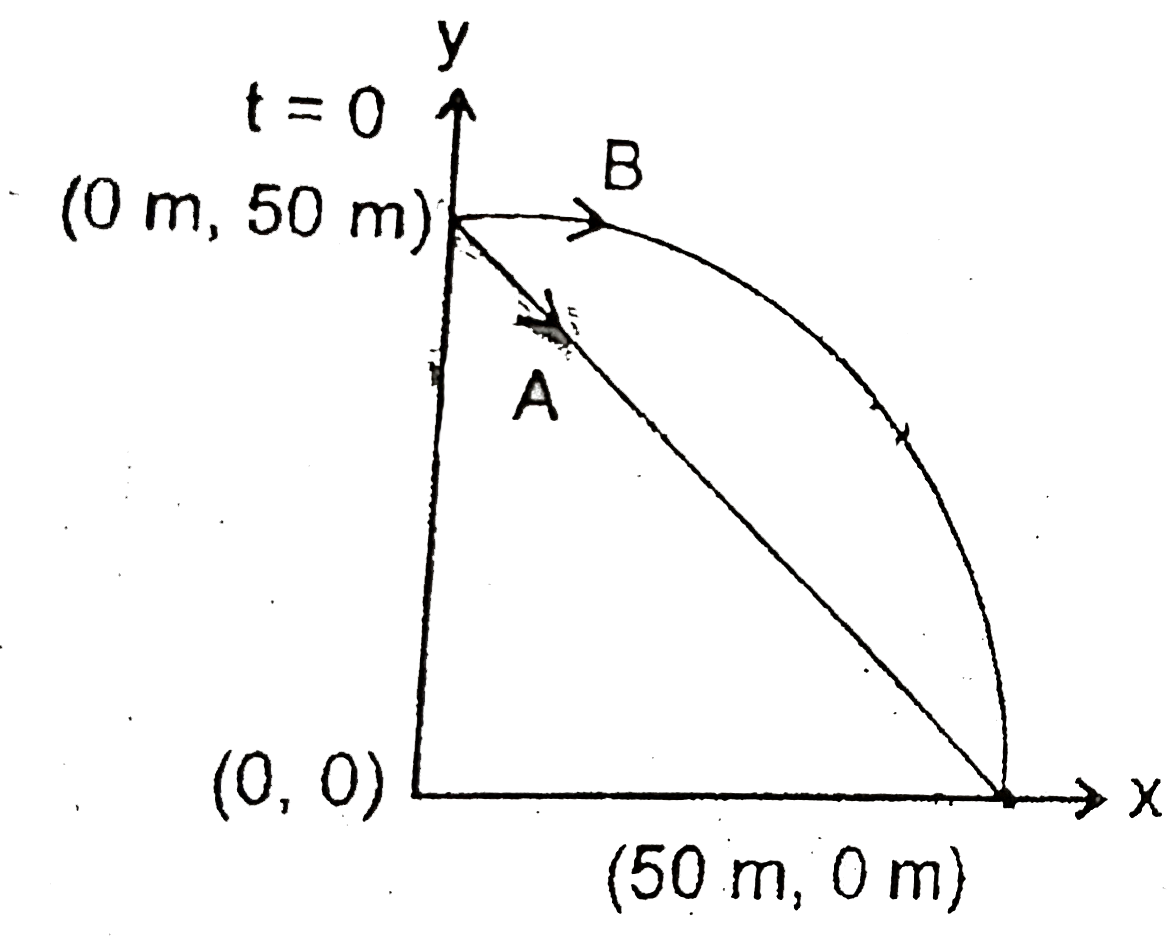
View Solution
