Consider two reactions having same Arrhenius factor A, but different energy of activation.
(i) A→B,Ea1=20kJ
(ii) C→D,Ea2=30kJ
Both are at temperature 25∘C It temperature in both reaction is increased slightly in such a way that change in temperature in both case is same than choose the correct options.
The second reaction is faster
The second reaction is more sensitive towards temperature variation
If temperature increases, rate of first reaction increase more sharply
All the above are correct
The correct Answer is:B
To solve the problem, we need to analyze the two reactions given their activation energies and the effect of temperature on their rates.
1. Identify the Given Data:
- Reaction 1: A→B with Ea1=20kJ/mol
- Reaction 2: C→D with Ea2=30kJ/mol
- Both reactions are at a temperature of 25∘C.
2. Understand the Arrhenius Equation:
The rate constant k for each reaction can be described by the Arrhenius equation:
k=Ae−EaRT
where:
- A = Arrhenius factor (same for both reactions)
- Ea = activation energy
- R = universal gas constant (approximately 8.314J/mol K)
- T = temperature in Kelvin
3. Convert Temperature to Kelvin:
The temperature in Kelvin is:
T=25∘C+273.15=298.15K
4. Analyze the Effect of Temperature Increase:
Let’s denote the increase in temperature for both reactions as ΔT. The new temperature for both reactions will be T+ΔT.
5. Evaluate the Rate Constants:
The rate constants for both reactions at the new temperature can be expressed as:
k′1=Ae−Ea1R(T+ΔT)
k′2=Ae−Ea2R(T+ΔT)
Since Ea1<Ea2, we can infer that k′1>k′2 at the original temperature.
6. Sensitivity to Temperature Changes:
The reaction with the lower activation energy (Reaction 1) will generally be more sensitive to temperature changes. This means that a small increase in temperature will lead to a relatively larger increase in the rate constant k′1 compared to k′2.
7. Conclusion:
- The first reaction (with Ea1=20kJ/mol) will have a higher rate constant than the second reaction (with Ea2=30kJ/mol) after the temperature increase.
- The second reaction is more sensitive to temperature variations, as the increase in temperature will cause a more significant change in the rate of the slower reaction.
Final Options Analysis:
Based on the analysis, the correct statements are:
- The first reaction is faster than the second reaction.
- The second reaction is more sensitive to temperature variations.
- Reaction 1: A→B with Ea1=20kJ/mol
- Reaction 2: C→D with Ea2=30kJ/mol
- Both reactions are at a temperature of 25∘C.
The rate constant k for each reaction can be described by the Arrhenius equation:
k=Ae−EaRT
where:
- A = Arrhenius factor (same for both reactions)
- Ea = activation energy
- R = universal gas constant (approximately 8.314J/mol K)
- T = temperature in Kelvin
The temperature in Kelvin is:
T=25∘C+273.15=298.15K
Let’s denote the increase in temperature for both reactions as ΔT. The new temperature for both reactions will be T+ΔT.
The rate constants for both reactions at the new temperature can be expressed as:
k′1=Ae−Ea1R(T+ΔT)
k′2=Ae−Ea2R(T+ΔT)
Since Ea1<Ea2, we can infer that k′1>k′2 at the original temperature.
The reaction with the lower activation energy (Reaction 1) will generally be more sensitive to temperature changes. This means that a small increase in temperature will lead to a relatively larger increase in the rate constant k′1 compared to k′2.
- The first reaction (with Ea1=20kJ/mol) will have a higher rate constant than the second reaction (with Ea2=30kJ/mol) after the temperature increase.
- The second reaction is more sensitive to temperature variations, as the increase in temperature will cause a more significant change in the rate of the slower reaction.
Based on the analysis, the correct statements are:
- The first reaction is faster than the second reaction.
- The second reaction is more sensitive to temperature variations.
Topper's Solved these Questions
Similar Questions
For the reaction at 298K
2A+B→C
ΔH=400kJmol−1 and ΔS=0.2kJK−1mol−1
At what temperature will the reaction becomes spontaneous considering ΔH and ΔS to be contant over the temperature range.
View SolutionFor two reactions (i) P→ Product and (ii) Q→ Product, the order of reaction (i) is 1 while that of reaction (ii) is 2. At 347K, the energy of activation of reaction (i) is 55kJmol−1 but whenever this reaction is carried out in the presence of catalyst at the same temperature, the energy of activation is 53kJmol−1. Moreover, for reaction (ii), when the temperature is increased form 298K to 308K, the rate of reaction increases as many times as for reaction (i) in the presnece of catalyst. Calculate the rate constant of reaction (ii) at 318K, if the pre-exponential factor for reaction (ii) is 3.56×109mol−1Ls−1.
Note: Arrhenius equation does not depend on the order of reaction.
View Solution
Knowledge Check
Two reactions having their energy of activation E1 and E2 temperature coefficients Tc1 and Tc2 respectively within the temperature 300 and 310K. The ratio of their temperature coefficient is:
AeE1/E2Be(E1−E2)×10−4/RC10E1/E2De(E1−E2)/4The activation energies for the two reactions are Ea and Ea′ with Ea>E′a. If the temperature of the reaction system is increased from T1 to T2. Predict which alternative is correct. (k′) are the rate constants at highest temperature.
Ak′1k+(1)=k′2k2Bk1<k2 and k′2<k′1Ck1<k2D(k′1k1)<2k′2k2The following graph depicts the effect of temperature on the activity of the two enzymes A and B that catalyze the same reaction. Choose the correct statement(s) for these results.
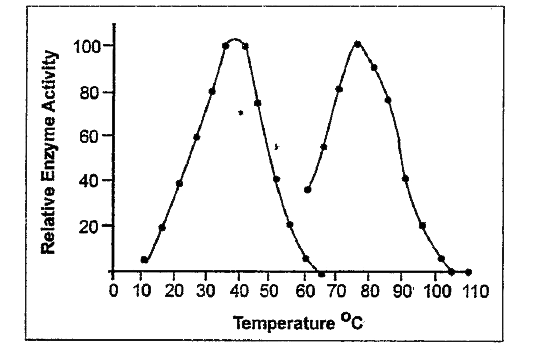
A. The rate of reaction in each case increases with increase in temperature and declines at higher temperatures due to denaturation of the enzyme.
B. Both the enzymes A and B are thermolabile.
C. At higher temperature, the reactants become highly energized and fail to interact with the active site, thus decreasing the rate of reaction.
D. The enzyme A is from a mesophilic organism, whereas the enzyme B is from a thermophilic organism.AA and BBB and CCC and DDA, B, D
For the reaction at 298K, 2A+B→C,ΔH=400kJmol−1,ΔS=0.2kJK−1mol−1. At what temperature will the reaction become spontaneous considering ΔHandΔS to be constant over the temperature range.
View SolutionThe rate of decomposition of a substance increases by a factor 2.25 for 1.5 times increases in concentration of substance at same temperature. Find order of the reaction
View SolutionTwo reactions of the same order have equal pre-exponential factors, but their activation energies differ by 24.9 kJ per mole. Calculate the ratio between the rate constants of these reactions at 27∘C.
View SolutionFor the reaction at 298 K
2A+B→C
ΔH=40kJmol−1 and ΔS=0.2kJK−1mol−1. At what temperature will the reaction beccomes sponatneous considering ΔH and ΔS to be constant over the temperature range.
View SolutionThe rate of reaction (dxdt) varies with nature, physical state and concentration of reactants, temperature, exposure to light and catalyst, whereas rate constant (K) varies with temperature and catalyst only. The rate constant K is given as K=Ae−Ea/RT where A is Arrhenius parameter or pre-exponential factor and Ea is energy of activation. The minimum energy required for a reaction is called threshold energy and the additional energy required by reactant molecules to attain threshold energy level is called energy of activation.
The temperature coefficient of reaction I is 2 and reaction II is 3. Both have same speed at 25∘C and show I order kinetics. The rati of rates of reaction of these two at 75∘C is:
View Solution
