Water from a hosepipe of radius 5 cm strikes a wall at a speed of 5ms−1 normally and stops. The force exerted on the wall in newton is
13.5π
6.25π
62.5π
27π
The correct Answer is:C
To solve the problem of finding the force exerted on the wall by water from a hosepipe, we will follow these steps:
Step 1: Convert the radius to meters
Given the radius of the hosepipe is 5 cm, we need to convert this to meters:
r=5 cm=5×10−2 m
Step 2: Calculate the cross-sectional area of the hosepipe
The cross-sectional area A of the circular hosepipe can be calculated using the formula:
A=πr2
Substituting the value of r:
A=π(5×10−2)2
A=π(25×10−4)
A=25π×10−4 m2
Step 3: Use the velocity of water
The speed v of the water is given as:
v=5 m/s
Step 4: Use the density of water
The density ρ of water is approximately:
ρ=1000 kg/m3
Step 5: Calculate the force exerted on the wall
The force F exerted on the wall can be calculated using the formula:
F=A⋅v2⋅ρ
Substituting the values we have:
F=(25π×10−4)⋅(52)⋅(1000)
F=(25π×10−4)⋅25⋅1000
F=625π×10−4⋅1000
F=625π×10−1
F=62.5π N
Step 6: Calculate the numerical value of the force
Using π≈3.14:
F≈62.5×3.14
F≈196.25 N
Final Answer
The force exerted on the wall is approximately:
F≈196.25 N
Given the radius of the hosepipe is 5 cm, we need to convert this to meters:
r=5 cm=5×10−2 m
The cross-sectional area A of the circular hosepipe can be calculated using the formula:
A=πr2
Substituting the value of r:
A=π(5×10−2)2
A=π(25×10−4)
A=25π×10−4 m2
The speed v of the water is given as:
v=5 m/s
The density ρ of water is approximately:
ρ=1000 kg/m3
The force F exerted on the wall can be calculated using the formula:
F=A⋅v2⋅ρ
Substituting the values we have:
F=(25π×10−4)⋅(52)⋅(1000)
F=(25π×10−4)⋅25⋅1000
F=625π×10−4⋅1000
F=625π×10−1
F=62.5π N
Using π≈3.14:
F≈62.5×3.14
F≈196.25 N
The force exerted on the wall is approximately:
F≈196.25 N
Topper's Solved these Questions
Similar Questions
Wind with a velocity 100kmh−1 blows normally against one of the walls of a house with an area of 108m2. Calculate the force exerted on the wall if the air moves parallel to the wall after striking it and has a density of 1.2kgm−3.
View SolutionA 3-kg steel ball strikes a wall with a speed of 10.0ms−1 at an angle of 60.0∘ with the surfaces of the wall. The ball bounces off with the same speed and same angle. If the ball was in contact with the wall for 0.2s, find the average force exerted by the wall on the ball.
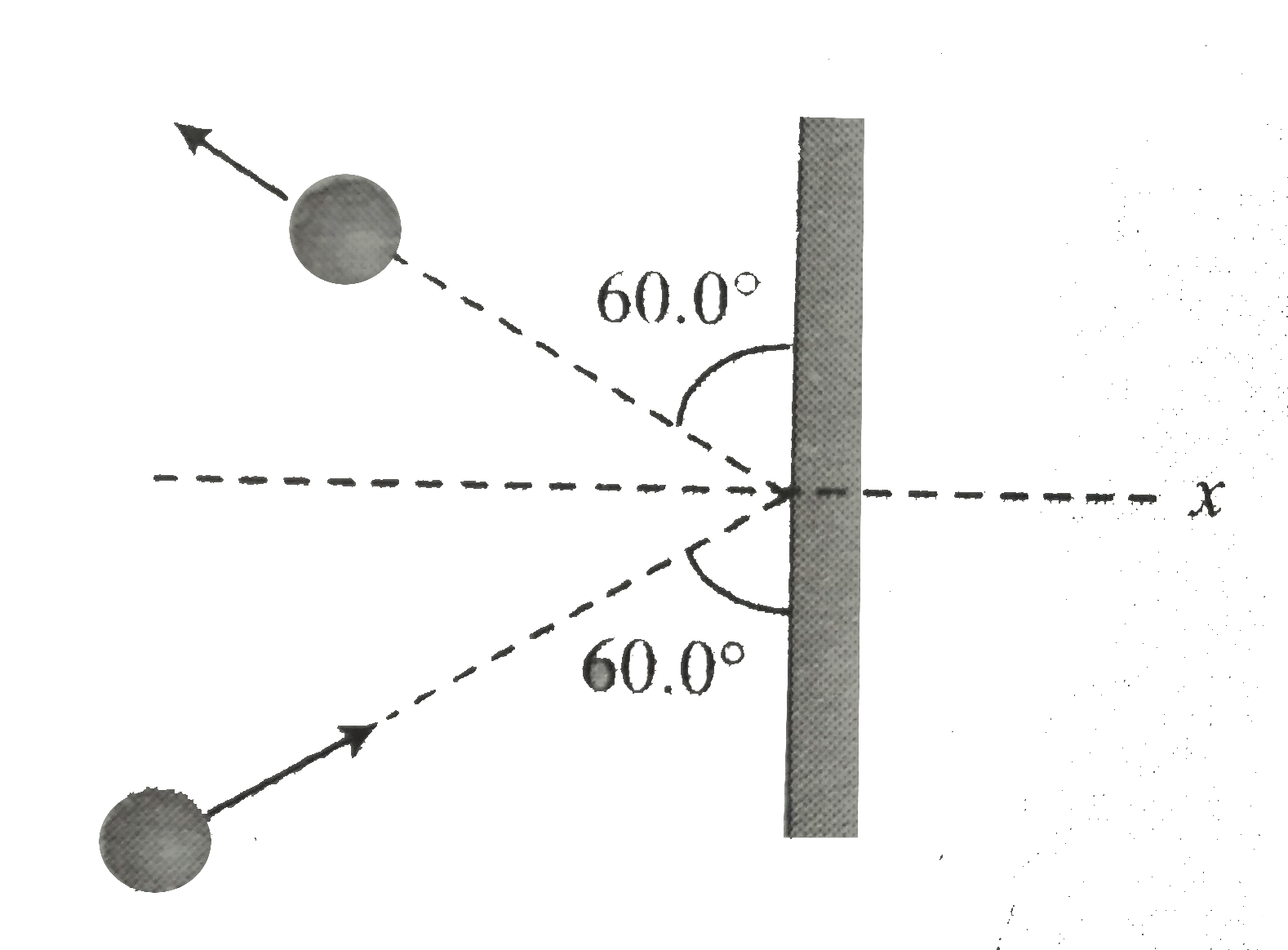
View Solution
Knowledge Check
A jet of water with cross section of 6cm2 strikes a wall at an angle of 60∘ to the normal and rebounds elastically from the wall without losing energy. If the velocity of the water in the jet is 12m/s, the force acting on the wall is
A0.864 NB86.4 NC72 ND7.2 NA ball of mass 0.1 kg strikes a wall normally with a speed of 30ms−1 and rebounds with a speed of 20ms−1. The impulse of the force exerted by the wall on the ball is
A1N−sB5N−sC2N−sD3N−sA horizontal jet of water coming out of a pipe of area of cross-section 20cm2 hits a vertical wall with a velocity of 10ms−1 and rebounds with the same speed. The force exerted by water on the wall is .
A0.2NB10NC400ND200N
The mass of hydrogen molecule is 3.23×1023 hydrogen molecules strike 2cm2 of a wall per second at an angle of 45∘ with the normal when moving with a speed of 105cms−1, what pressure do they exert on the wall ? Assume collision to be elasitc.
View SolutionA block of weight 5N is pushed against a vertical wall by a force 12 N. The coefficient of friction between the wall and block is 0.6. The magnitude of the force exerted by the wall on the block is
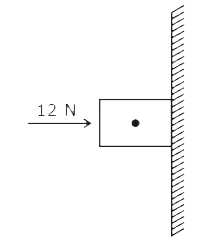
View SolutionA hammer weighing 3 kg strikes the head of a nail with a speed of 2ms−1 drives it by 1 cm into the wall. The impulse imparted to the wall is
View SolutionA 1.5 kg ball drops vertically on a floor hitting with a speed of 25 ms1. It rebounds with an initial speed of 15ms−1. If the ball was in contact for only 0.03, the force exerted on the floor by the ball is
View SolutionA jet water, whose cros section is 'a' strikes a wall making an angle θ with normal and elastically rebounds. The velocity of water of density 'd' is v. Force exerted on wall is :-
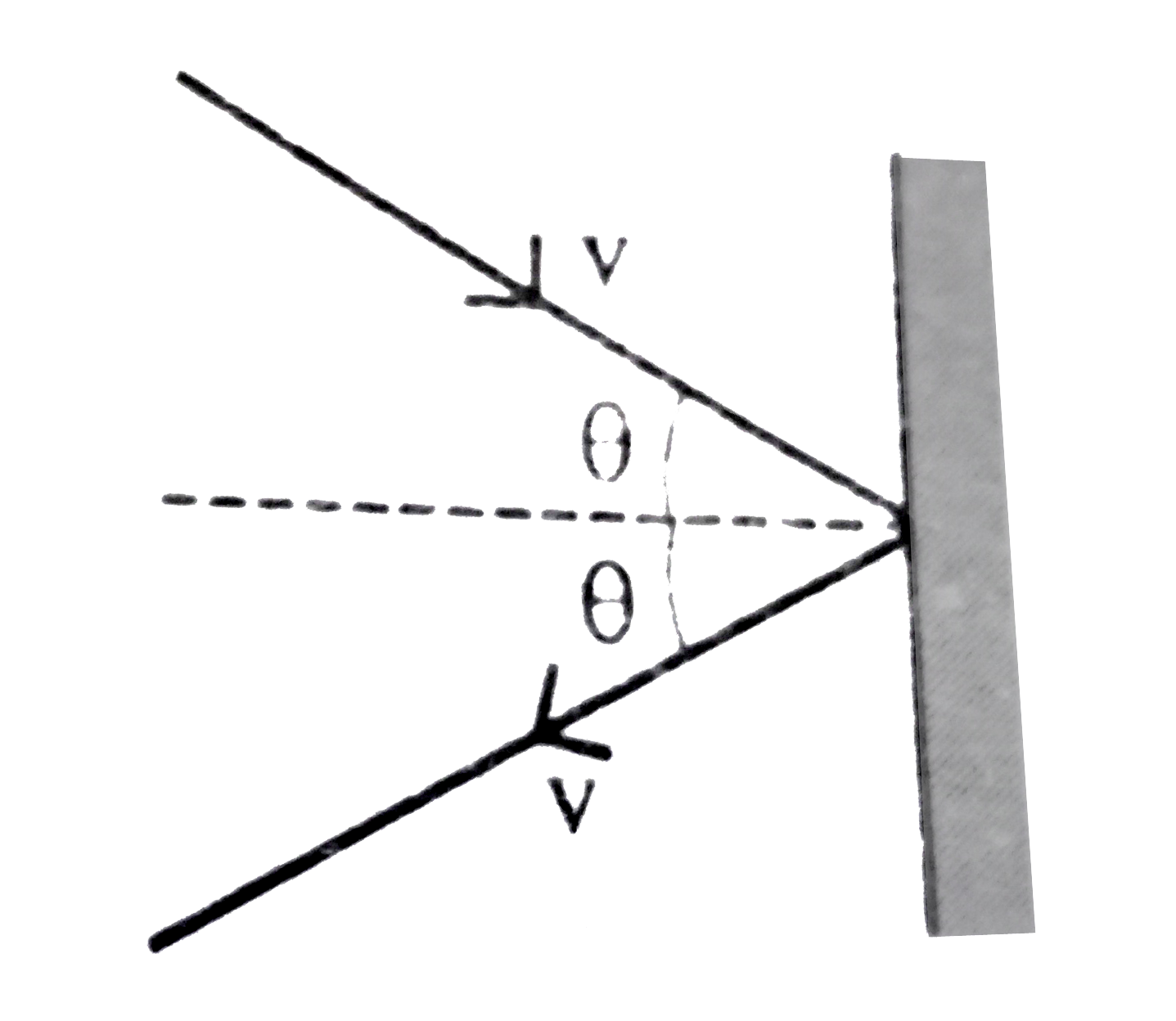
View Solution