Consider a torod , having a circular cross-section of radius b, major radius R ( R > > b), having N turns and carrying current I. Find the total energy stored in the toroid.
μ0N2I2b22R
μ0N2I2b23R
μ0N2I2b26R
μ0N2I2b24R
The correct Answer is:D
To find the total energy stored in a toroid with a circular cross-section, we can follow these steps:
Step 1: Understand the Geometry of the Toroid
A toroid has a circular cross-section with a radius b and a major radius R. Given that R≫b, we can treat the toroid as a solenoid wrapped around a circular path.
Step 2: Determine the Magnetic Field Inside the Toroid
The magnetic field B inside a toroid is given by the formula:
B=μ0NI2πR
where μ0 is the permeability of free space, N is the number of turns, and I is the current flowing through the toroid.
Step 3: Calculate the Area of the Cross-Section
The area A of the circular cross-section of the toroid is:
A=πb2
Step 4: Calculate the Magnetic Flux
The magnetic flux Φ through one turn of the toroid is given by:
Φ=B⋅A=(μ0NI2πR)⋅(πb2)=μ0NIb22R
Since there are N turns, the total magnetic flux linked with the toroid is:
Φtotal=NΦ=N⋅μ0NIb22R=μ0N2Ib22R
Step 5: Calculate the Inductance of the Toroid
The inductance L of the toroid can be calculated using the formula:
L=ΦtotalI=μ0N2Ib22RI=μ0N2b22R
Step 6: Calculate the Energy Stored in the Toroid
The energy U stored in an inductor is given by:
U=12LI2
Substituting the expression for L:
U=12(μ0N2b22R)I2=μ0N2b2I24R
Final Result
The total energy stored in the toroid is:
U=μ0N2b2I24R
---
A toroid has a circular cross-section with a radius b and a major radius R. Given that R≫b, we can treat the toroid as a solenoid wrapped around a circular path.
The magnetic field B inside a toroid is given by the formula:
B=μ0NI2πR
where μ0 is the permeability of free space, N is the number of turns, and I is the current flowing through the toroid.
The area A of the circular cross-section of the toroid is:
A=πb2
The magnetic flux Φ through one turn of the toroid is given by:
Φ=B⋅A=(μ0NI2πR)⋅(πb2)=μ0NIb22R
Since there are N turns, the total magnetic flux linked with the toroid is:
Φtotal=NΦ=N⋅μ0NIb22R=μ0N2Ib22R
The inductance L of the toroid can be calculated using the formula:
L=ΦtotalI=μ0N2Ib22RI=μ0N2b22R
The energy U stored in an inductor is given by:
U=12LI2
Substituting the expression for L:
U=12(μ0N2b22R)I2=μ0N2b2I24R
The total energy stored in the toroid is:
U=μ0N2b2I24R
Topper's Solved these Questions
Similar Questions
A toroid with mean radius r0, diameter 2a have N turns carrying current l. What is the magnetic field B inside the the toroid?
View SolutionFigure shows a conductor of length l having a circular cross-section. The radius of cross-section varies linearly from a to b. Find the resistance of the conductor. ltbtgt

View Solution
Knowledge Check
Consider a toroid of circular cross - section of radius b, major radius R much greater than minor radius b, (see diagram) find the total energy stored in magnetic field of toroid -
 AB2π2b2R2μ0BB2π2b2R4μ0CB2π2b2R8μ0DB2π2b2Rμ0
AB2π2b2R2μ0BB2π2b2R4μ0CB2π2b2R8μ0DB2π2b2Rμ0A circular coil of radius 10 cm having 100 turns carries a current of 3.2 A. The magnetic field at the center of the coil is
A2.01×10−3TB5.64×10−3TC2.64×10−3TD5.64×10−3TA long straight wire of a circular cross-section (radius a) carries a steady current I and the current I is uniformly distributed across this cross-section. Which of the following plots represents the variation of magnitude of magnetic field B with distance r from the centre of the wire?
A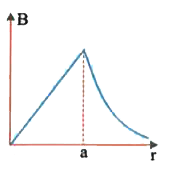 B
B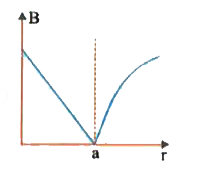 C
C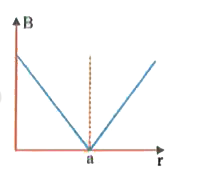 D
D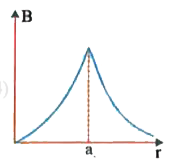
Figure shows a long straight wire of a circular cross-section (radius a) carrying steady current l. The current l is uniformly distributed across this cross-section. Calculate the magnetic field in the region r<aandr>a

View SolutionA toroid of mean radius 'a', cross section radius 'r' and total number of turns N. It carries a current 'I'. The torque experienced by the toroid if a uniform magnetic field of strength B is applied.
View SolutionA circular coil of n turns and radius r carries a current I. The magnetic field at the center is
View SolutionA toroid having 200 turns carries a current of 1A. The average radius of the toroid is 10 cm. the magnetic field at any point in the open space inside the toroid is
View SolutionFigure A and B shown two long straight wires of circular cross-section (a and b with a<b), carrying current I which is uniformly distributed across the cross-section. The magnitude of magnetic field B varies with radius r and can be represented as :
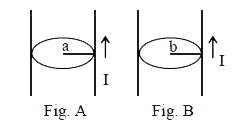
View Solution
