A block of mass 2 kg is having velocity 4√5ms−1 in the positive x - direction at the origin. The only force acting on it is F=(3x2−12x)N. Its velocity when it is at x=2 m is
8ms−1
4ms−1
10√24ms−1
20ms−1
The correct Answer is:A
To find the velocity of the block when it is at x=2 m, we will use the work-energy principle, which states that the work done by the forces acting on an object is equal to the change in its kinetic energy.
1. Identify the Given Data:
- Mass of the block, m=2kg
- Initial velocity at x=0, v0=4√5m/s
- Force acting on the block, F=3x2−12xN
2. Calculate the Initial Kinetic Energy:
KE0=12mv20=12×2×(4√5)2=1×80=80J
3. Calculate the Work Done by the Force from x=0 to x=2:
The work done W can be calculated by integrating the force over the displacement:
W=∫20(3x2−12x)dx
- Calculate the integral:
W=(x3−6x2)20=(23−6(22))−(0−0)=8−24=−16J
4. Calculate the Final Kinetic Energy:
The work-energy principle states:
KEf=KE0+W
KEf=80J−16J=64J
5. Calculate the Final Velocity:
Using the final kinetic energy to find the final velocity vf:
KEf=12mv2f
64=12×2×v2f⟹64=v2f⟹vf=√64=8m/s
Final Answer:
The velocity of the block when it is at x=2m is 8m/s.
- Mass of the block, m=2kg
- Initial velocity at x=0, v0=4√5m/s
- Force acting on the block, F=3x2−12xN
KE0=12mv20=12×2×(4√5)2=1×80=80J
The work done W can be calculated by integrating the force over the displacement:
W=∫20(3x2−12x)dx
W=(x3−6x2)20=(23−6(22))−(0−0)=8−24=−16J
The work-energy principle states:
KEf=KE0+W
KEf=80J−16J=64J
Using the final kinetic energy to find the final velocity vf:
KEf=12mv2f
64=12×2×v2f⟹64=v2f⟹vf=√64=8m/s
The velocity of the block when it is at x=2m is 8m/s.
Topper's Solved these Questions
Similar Questions
A block of mass 2 kg is moving with a velocity of 2ˆi−ˆj+3ˆk m/s. Find the magnitude and direction of momentum of the block with the x-axis.
View Solution50.A body of mass 2kg is moving along positive X - direction with a velocity of 5ms^(-1) . Now a force of 10sqrt(2)N is applied at an angle 45^(@) with X -axis.Its velocity after 3s is.
View Solution
Knowledge Check
A block of mass 2 kg is kept at origin at t = 0 and is having velocity 4√5m/s in positive x - direction. The only force on it is a conservative and its potential energy is defined as U=−x3+6x2+15 (SI units). Its velocity when the force acting on it is minimum (after the time t = 0 ) is
A8m/sB4m/sC10√24m/sDnone of theseA body of mass 0.4kg starting at origin at t=0 with a speed of 10ms−1 in the positive x-axis direction is subjected to a constant F=8 N towards negative x-axis.
A−6000mB−8000mC+4000mD+7000mA block of the mass of 1 kg is moving on the x -axis. A force F acting on the block is shown. The veloity of the block at time t = 2 s is −3ms−1. What is the speed of the block at time t = 4 s?
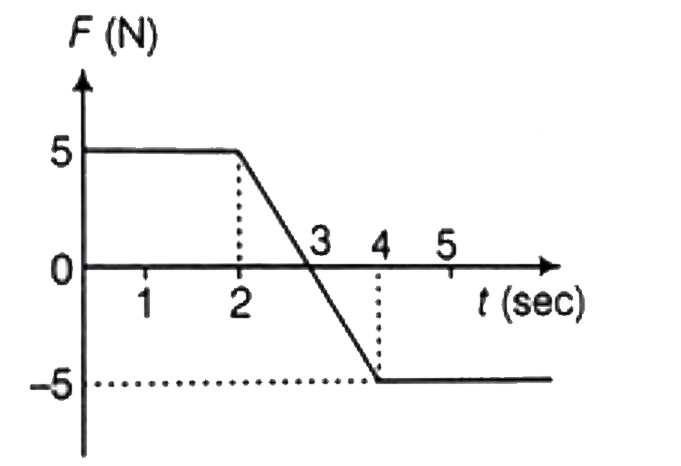 A8ms−1B2ms−1C3ms−1D5ms−1
A8ms−1B2ms−1C3ms−1D5ms−1
As a 2.5 kg body moves in the positive direction along an x axis, a single force acts on it. The force is given by Fx=−6xN, with x in meters. The velocity at x=3.5m is 8.5 m/s. (a) Find the velocity of the body at x=4.5 m. (b) Find the positive value of x at which the body has a velocity of 5.5 m/s.
View SolutionA block of mass 4kg is initially at rest on a horizontal frixtionless surface. A horizontal force →F=(3+x)ˆi newtons acts on it, when the block is at x=0. The maximum kinetic energy of the block between x=0 and x=2m is
View SolutionAn object of mass 40 kg and having velocity 4ms−1 collides with another object of mass 60 kg. having velocity 2 ms−1 The loss of kinetic energy when the collision is perfectly ineleastic is
View SolutionA particle A of mass 10/7kg is moving in the positive direction of x−aξs. At initial position x=0, its velocity is 1ms−1, then its velocity at x=10m is (use the graph given)

View SolutionA ball of mass 0.5 kg is moving with a velocity of 2ms−1. It if subjected to a force of x Newton for 2s. Because of this force, the ball moves with a velocity of 3ms−1 . The value of x is :
View Solution