In a circular motion of a particle , the tangential acceleration of the particle is given by at=9ms−2 . The radius of the circle is 4m . The particle was initially at rest. Time after which total acceleration of the particle makes an angle of 45∘ with the radial acceleration is
13s
23s
53s
43s
The correct Answer is:B
To solve the problem step-by-step, we will analyze the circular motion of the particle and use the information given to find the time after which the total acceleration makes an angle of 45 degrees with the radial acceleration.
Step 1: Understand the Components of Acceleration
In circular motion, the total acceleration A of a particle can be broken down into two components:
- Tangential Acceleration at: This is the acceleration along the tangent to the circular path, which is given as at=9m/s2.
- Radial (Centripetal) Acceleration ar: This is directed towards the center of the circular path and is given by the formula:
ar=v2r
where v is the tangential velocity and r is the radius of the circular path.
Step 2: Set Up the Condition for the Angle
We are given that the total acceleration makes an angle of 45∘ with the radial acceleration. This means:
tan(45∘)=1=atar
Thus, we can write:
at=ar
Step 3: Calculate the Radial Acceleration
Substituting the expression for radial acceleration:
at=v2r
Given at=9m/s2 and r=4m, we have:
9=v24
Multiplying both sides by 4 gives:
v2=36
Taking the square root, we find:
v=6m/s
Step 4: Relate Velocity to Time
The tangential acceleration is constant, and it is related to the change in velocity over time:
at=dvdt
Substituting at=9m/s2:
9=dvdt
Integrating this from the initial velocity (which is 0, since the particle starts from rest) to the final velocity v:
∫v0dv=∫t09dt
This gives:
v=9t
Substituting v=6m/s:
6=9t
Solving for t:
t=69=23s
Step 5: Conclusion
The time after which the total acceleration of the particle makes an angle of 45∘ with the radial acceleration is:
23s
In circular motion, the total acceleration A of a particle can be broken down into two components:
- Tangential Acceleration at: This is the acceleration along the tangent to the circular path, which is given as at=9m/s2.
- Radial (Centripetal) Acceleration ar: This is directed towards the center of the circular path and is given by the formula:
ar=v2r
where v is the tangential velocity and r is the radius of the circular path.
We are given that the total acceleration makes an angle of 45∘ with the radial acceleration. This means:
tan(45∘)=1=atar
Thus, we can write:
at=ar
Substituting the expression for radial acceleration:
at=v2r
Given at=9m/s2 and r=4m, we have:
9=v24
Multiplying both sides by 4 gives:
v2=36
Taking the square root, we find:
v=6m/s
The tangential acceleration is constant, and it is related to the change in velocity over time:
at=dvdt
Substituting at=9m/s2:
9=dvdt
Integrating this from the initial velocity (which is 0, since the particle starts from rest) to the final velocity v:
∫v0dv=∫t09dt
This gives:
v=9t
Substituting v=6m/s:
6=9t
Solving for t:
t=69=23s
The time after which the total acceleration of the particle makes an angle of 45∘ with the radial acceleration is:
23s
Topper's Solved these Questions
Similar Questions
In a circular motion of a particle , the tangential acceleration of the particle is given by at=9ms−2 . The radius of the circle is 4m . The particle was initially at rest. Time after which total acceleration of the particle makes an angle of 45∘ with the radial acceleration is
View SolutionIn a circular motion of a particle the tangential acceleration of the particle is given by at=2tm/s2. The radius of the circle described is 4m. The particle is initially at rest. Time after which total acceleration of the particle makes 45∘ with radial acceleration is :
View Solution
Knowledge Check
The tangenital acceleration of a particle in a circular motion of radius 2 m is at=αtm/s2 (where α is a constant) initially the particle as rest. Total acceleration of the particle makes 45∘ with the radial acceleration after 2 sec The value of constant α is :
A12m/s3B1m/s3C2m/s3DData are insufficientFor a particle in circular motion the centripetal acceleration is
ALess than its tangential accelerationBEqual to its tangential accelerationCMore than its tangential accelerationDMay be more or less than its tangential accelerationVelocity of a particle is given as v=(2t2−3)m/s. The acceleration of particle at t = 3s will be :
A18ms−2B12ms−2C15ms−2Dzero
Tangental acceleration of a particle moving in a circle of radius 1 m varies with time t as shown in figure (initial velocity of the particle is zero). Time after which total acceleration of particle makes an angle of 30∘ with radial acceleration is
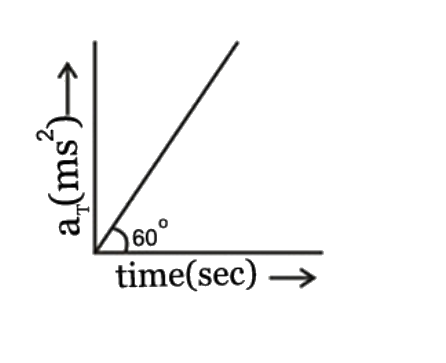
View SolutionA particle is moving on a circular path of radius 1m. It starts from rest,its tangential acceleration is √3t .The time after which the acceleration of the particle makes an angle of 30∘ with centripetal acceleration is (n)23s .Find the value of n.
View SolutionThe tangential and radial acceleration of a particle are a(t) and a(r) respectively. The motion of a particle is circular if
View SolutionThe acceleration of a particle varies with time t as
a=t2+t+2
where t is in seconds.
The particle starts with an initial velocity v-3m/s at t=0. find the velocity of the particle at the end of 5s.
View SolutionIn a non - uniform circular motaion the ratio of tangential to radial acceleration is (where, r= radius of circle, v= speed of the particle, α= angular acceleration)
View Solution
