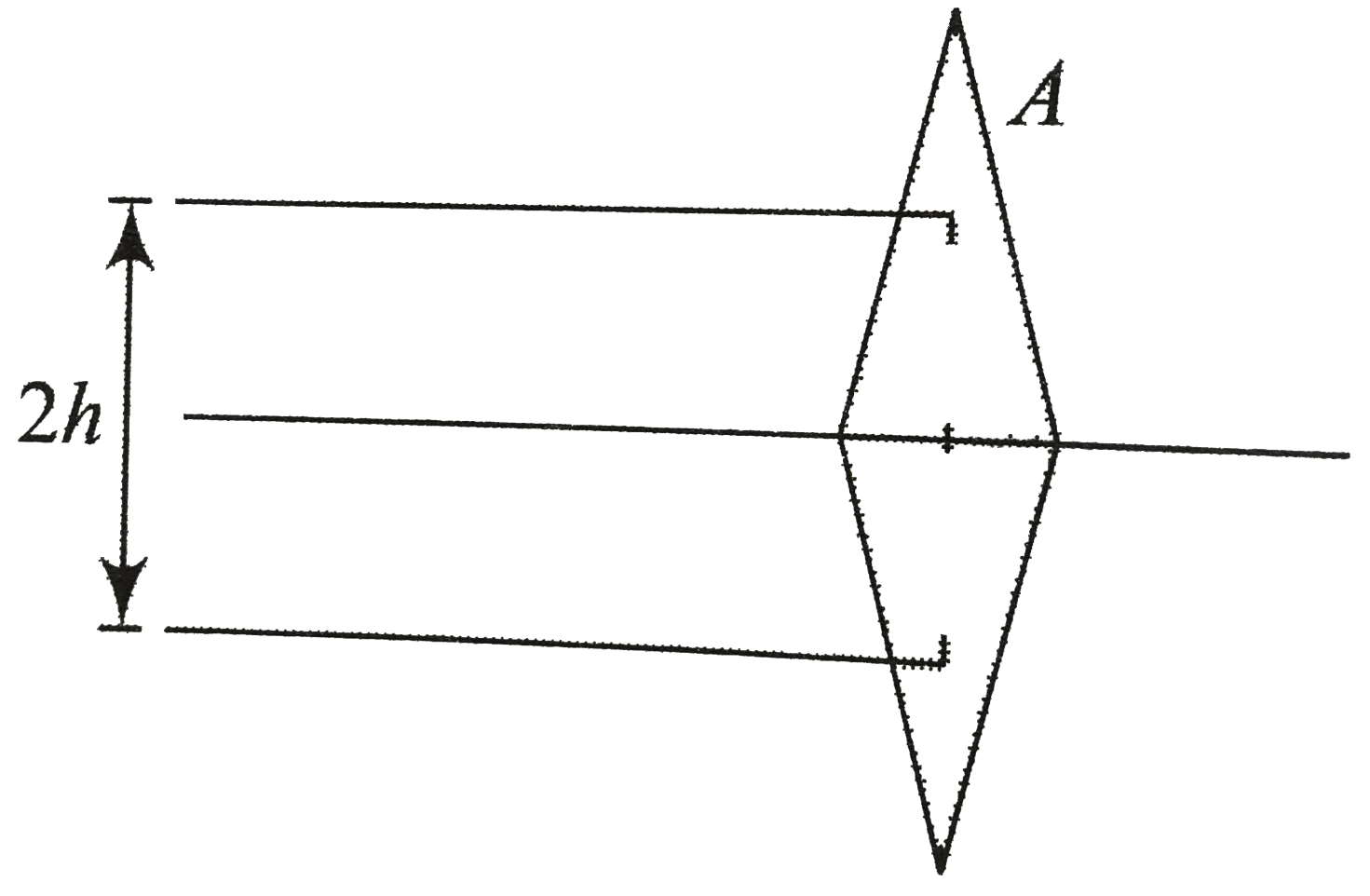
Two identical thin isosceles prims of refracting angle and refractive index are placed with their bases touching each other. A parallel beam , of width 2b, is incident on this system , as shown. The distance of the point of convergence from the prism is

The correct Answer is:A
Step by step video & image solution for Two identical thin isosceles prims of refracting angle theta and refractive index mu are placed with their bases touching each other. A parallel beam , of width 2b, is incident on this system , as shown. The distance of the point of convergence from the prism is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Two identical thin isosceles prisms of refracting angle A and refractive index μ are placed with their bases touching each other and this system can collectively act as a crude converging lens. A parallel beam of light is incident on this system as shown in Figure. Find the focal length of this so called converging lens.
View SolutionA thin prism of refracting angle 2∘ deviates an incident ray through an angle of 1∘.Find the value of refractive index of material of prism.
View Solution
Knowledge Check
Two isosceles prism of prism angle A and refractive index μ are placed with their bases touching each other. This system can act as a crude converging lens. The focal length of the lens for A=10∘,μ=1.5 and a ray of light incident on a prims at a height of 1 cm from its base, is approximately.
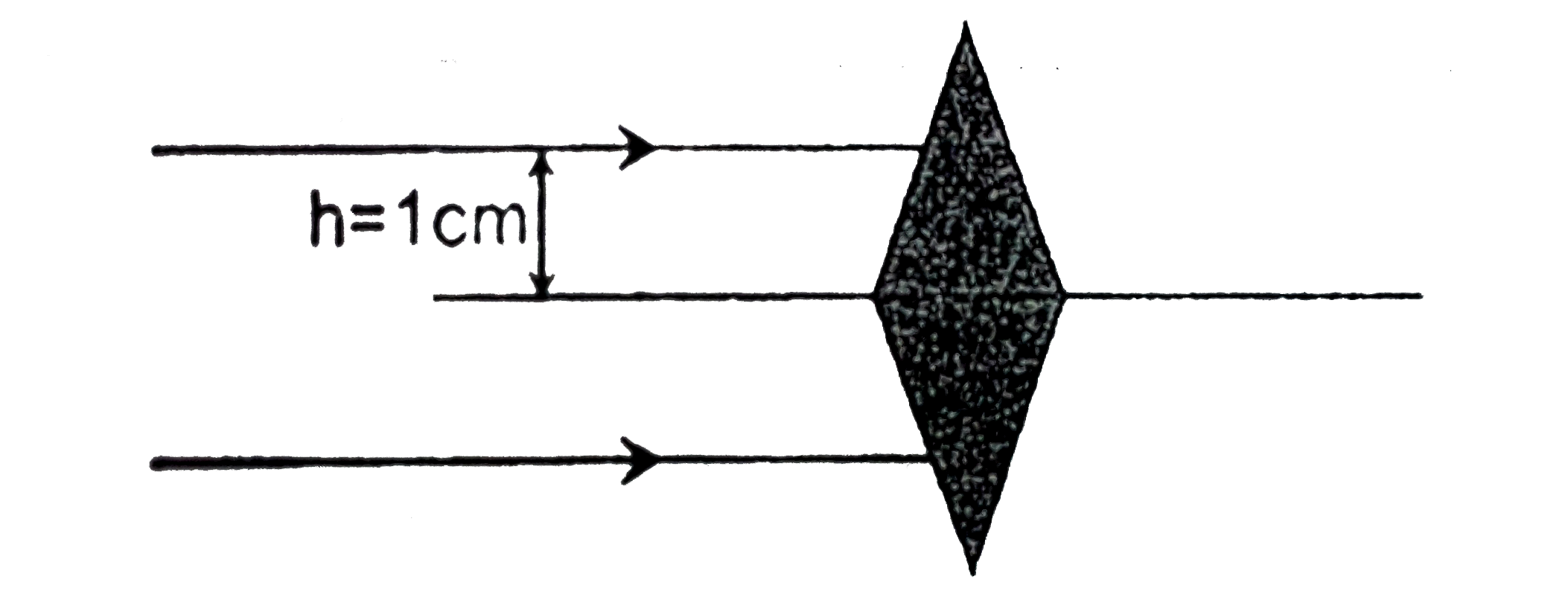 A11.5 cmB23.0cmCzeroD5.75cm
A11.5 cmB23.0cmCzeroD5.75cm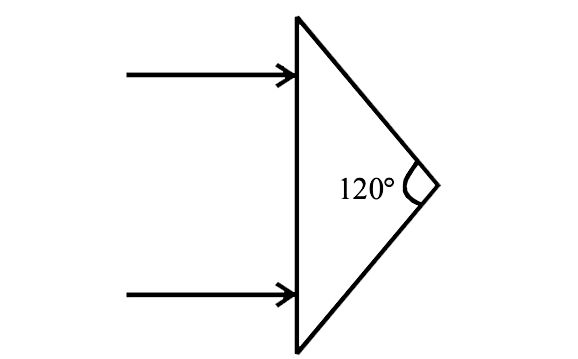
An isosceles prism of angle 120degree has a refractive index 1.44. Two parallel monochromatic rays enter the prism parallel to each other in air as shown. The rays emerge from the opposite facesAare parallel to each otherBare divergingCmake an angle 2[sin−1(0.72)−30degree] with each otherDmake an angle 2sin−1(0.72) with each otherA clear transparent glass sphere (μ=1.5) of radius R is immersed in a liquid of refractive index 1.25. A parallel beam of light incident on it will converge to a point. The distance of this point from the center will be
A−3RB+3RC−RD+R
The refractive index of a prism is μ. Find the maximum angle of the prism for which a ray incident on it will be transmitted through other face without total internal reflection.
View SolutionA prism having refractive index √2 and refractive angle 30∘ has one of the refractive surfaces polished. A beam of light incident on the other surfaces will trace its path if the angle of incidence is
View SolutionFor an angle of incidence θ on an equilateral prism of refractive index √3, the ray refracted is parallel to the base inside the prism. The value of θis
View SolutionA prism having refractive index √2 and refracting angle 30∘, has one of the refracting surfaces polished. A beam of monochromatic light incident on the other refracting surface will retrace its path if the angle of incidence is
View SolutionA prism of apex angle A=60∘ has the refractive index μ=√2. The angle of incidence for minimum deviation is
View Solution
