A biconvex lens of focal length 40 cm is placed in front of an object at a distance of 20 cm . Now a slab of refractive index 43 is placed somewhere in between the lens and the object. The shift in the image formed after the introduction of slab equals (thickness of the slab is 2 mm)
1 mm
2 mm
3 mm
4 mm
The correct Answer is:B
To solve the problem step by step, we will follow these instructions:
Step 1: Identify the parameters
- Focal length of the biconvex lens (f) = 40 cm
- Object distance (u) = -20 cm (the negative sign indicates that the object is on the same side as the incoming light)
- Refractive index of the slab (μ) = 4/3
- Thickness of the slab (t) = 2 mm = 0.2 cm (converting mm to cm for consistency)
Step 2: Use the lens formula to find the initial image position (without the slab)
The lens formula is given by:
1f=1v−1u
Rearranging gives:
1v=1f+1u
Substituting the values:
1v=140+1−20
Finding a common denominator (LCM of 40 and 20 is 40):
1v=140−240=−140
Thus,
v=−40 cm
This indicates that the image is formed 40 cm on the same side as the object.
Step 3: Calculate the shift due to the slab
The shift (Δ) caused by the slab can be calculated using the formula:
Δ=t(1−1μ)
Substituting the values:
Δ=0.2(1−34)=0.2(14)=0.05 cm=0.5 mm
Step 4: Calculate the new object distance after introducing the slab
The effective object distance (u') after introducing the slab is:
u′=u+Δ
Substituting the values:
u′=−20+0.05=−19.95 cm
Step 5: Use the lens formula again to find the new image position (v')
Using the lens formula again:
1v′=1f+1u′
Substituting the values:
1v′=140+1−19.95
Finding a common denominator (LCM of 40 and 19.95):
1v′=140−119.95
Calculating the right-hand side:
1v′≈0.0251−0.0501251≈−0.025125
Thus,
v′≈−39.7 cm
Step 6: Calculate the shift in the image position
The shift in the image position (Δv) is given by:
Δv=v′−v
Substituting the values:
Δv=−39.7−(−40)=0.3 cm=3 mm
Final Result
The total shift in the image formed after the introduction of the slab is approximately 2 mm.
- Focal length of the biconvex lens (f) = 40 cm
- Object distance (u) = -20 cm (the negative sign indicates that the object is on the same side as the incoming light)
- Refractive index of the slab (μ) = 4/3
- Thickness of the slab (t) = 2 mm = 0.2 cm (converting mm to cm for consistency)
The lens formula is given by:
1f=1v−1u
Rearranging gives:
1v=1f+1u
Substituting the values:
1v=140+1−20
Finding a common denominator (LCM of 40 and 20 is 40):
1v=140−240=−140
Thus,
v=−40 cm
This indicates that the image is formed 40 cm on the same side as the object.
The shift (Δ) caused by the slab can be calculated using the formula:
Δ=t(1−1μ)
Substituting the values:
Δ=0.2(1−34)=0.2(14)=0.05 cm=0.5 mm
The effective object distance (u') after introducing the slab is:
u′=u+Δ
Substituting the values:
u′=−20+0.05=−19.95 cm
Using the lens formula again:
1v′=1f+1u′
Substituting the values:
1v′=140+1−19.95
Finding a common denominator (LCM of 40 and 19.95):
1v′=140−119.95
Calculating the right-hand side:
1v′≈0.0251−0.0501251≈−0.025125
Thus,
v′≈−39.7 cm
The shift in the image position (Δv) is given by:
Δv=v′−v
Substituting the values:
Δv=−39.7−(−40)=0.3 cm=3 mm
The total shift in the image formed after the introduction of the slab is approximately 2 mm.
Topper's Solved these Questions
Similar Questions
A point object is placed at a distance of 25cm from a convex lens. Its focal length is 22cm. A glass slab of refractive index 1.5 is inserted between the lens and the object, then the image is formed at infinity. Find the thickness of the glass slab (in cm).
View SolutionA point object is placed at a distance of25cmfrom a convex lens of focal length 20cm.If a glass slab of thicknesstand refractive index 1.5is inserted between the lens and object.The image is formed at infinity .Find the thickness?
View Solution
Knowledge Check
A convex lens of focal length 15 cm is placed on a plane mirror. An object is placed 20 cm from the lens. The image is formed
A12 cm in front of the mirrorB60 cm behind the mirrorC60 cm in front of the mirrorD30 cm in front of the mirrorA point object is placed at a distance of 25 cm from a convex lens of focal length 20cm. If a glass slab of thickness t and refractive index 1.5 is inserted between the lens and the object, the image is formed at infinity. The thickness t is
A10cmB5cmC20cmD15cmA convex lens has a focal length of 20 cm. It is used to form an image of an object placed 15 cm from lens. The image is
Avirtual inverted and enlargeBreal,inverted and diminishedCreal,inverted and enlargeDvirtual,erect and enlarge
A convex lens of focal length 20cm is placed 10cm in front of a convex mirror or radius of curvature 15cm. Where should a point object be placed in front of the lens so that it images on to itself?
View SolutionA convex lens of focal length f1 is placed in front of a luminous point object. The separation between the object and the lens is 3f1 . A glass slab of thikness t is placed between the object and the lens. A real image of the object is formed at the shortest possible distance from the object.
a. Find the refractive index of the slab.
b. If a concave lens of very large focal length f2 is placed in contact with the convex lens, find the shifting of the image.
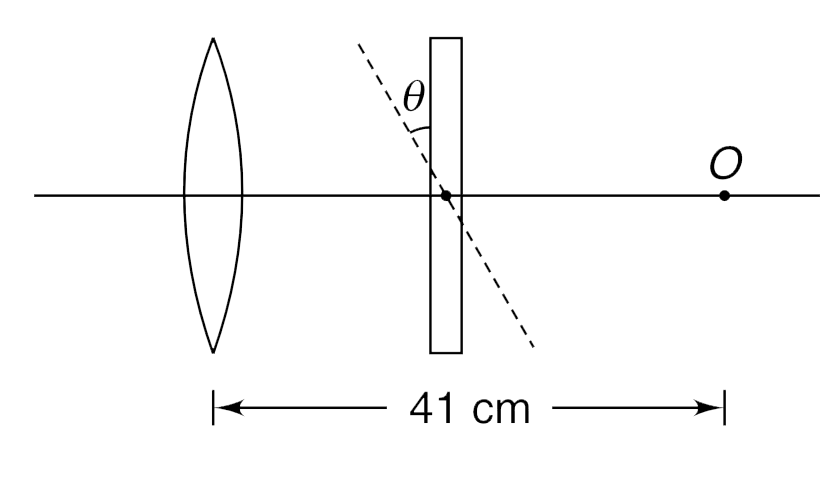
View SolutionA point object O is placed at a distance of 41 cm from a convex lens of focal length f=20 cm on its principal axis. A glass slab of thickness 3 cm and refractive index μ=1.5 is placed between the lens and the object with its faces perpendicular to the principal axis of the lens. Image of the object is formed at point I1. Now the glass slab is tilted by an angle of θ=1° (as shown in the Figure) and the final image is formed at I2. Calculate the distance between points I1 and I2. Consider only paraxial rays for the lens and near normal incidence for the glass slab.
View SolutionA point object is placed at a diatance of 25 cm from a convex lens of focal length 20 cm. If a glass slab of thickness t and refractive index 1.5 is inserted between the lens and the object, the image is formed at infinity. The thickness t is
View SolutionA point object is placed at a distance of 25cm from a convex lens of focal length 20cm .If a glass slab of thickness t and refractive index 1.5 is inserted between the lens and object.The image is formed at infinity .Find the thickness?
View Solution
