An ideal gas (1 mol ,monatomic) is in the initial state P (see diagram) on an isothermal curve A at a temperature T0 . It is brought under a constant volume (2V0) process to Q which lies on an adiabatic curve B intersecting the isothermal curve A at (P0,V0,T0) . The change in the internal energy of the gas (in terms of T0 ) during the process is (22/3=1.587)

2.3T0
−4.6T0
−2.3T0
4.6T0
The correct Answer is:B
Step by step video & image solution for An ideal gas (1 mol ,monatomic) is in the initial state P (see diagram) on an isothermal curve A at a temperature T_0 . It is brought under a constant volume (2V_0) process to Q which lies on an adiabatic curve B intersecting the isothermal curve A at (P_0,V_0,T_0) . The change in the internal energy of the gas (in terms of T_0 ) during the process is (2^(2//3)=1.587) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A quantity of gas occupies an initial volume V0 at pressure p0 and temperature T0. It expands to a volume V (a) constant temperature and (b) constant pressure. In which case does the gas do more work ?

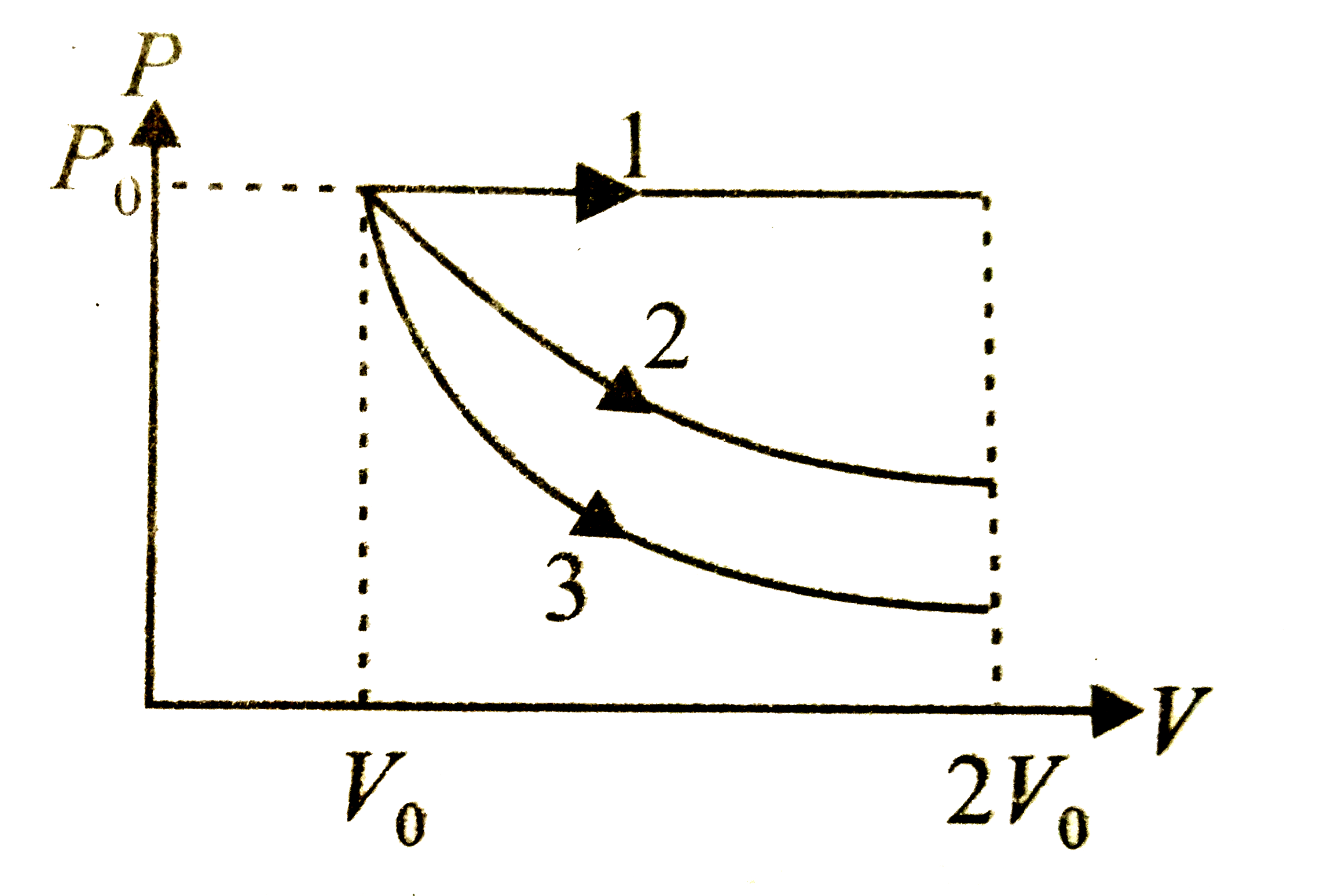
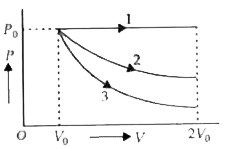
View SolutionA gas is expanded form volume V0→2V0 under three different processes as shown in the figure . Process 1 is isobaric process process 2 is isothermal and and process 3 is adiabatic .
Let ΔU1,ΔU2andΔU3 be the change in internal energy of the gs in these three processes then
View Solution
Knowledge Check
An ideal gas (1 mol, monatomic) is in the intial state P (see Fig.) on an isothermal A at temperature T0. It is brought under a constant volume (2V0) process to Q which lies on an adiabatic B intersecting the isothermal A at (P0,V0,T0). The change in the internal energy of the gas during the process is (in terms of T0)(22/3=1.587)
 A2.3T0B−4.6T0C−2.3T0D4.6T0
A2.3T0B−4.6T0C−2.3T0D4.6T0One mole of hydrogen, assumed to be ideal, is adiabatically expanded from its initial state (P1,V1,T1) to the final state (P2,V2,T2). The decrease in the internal energy of the gas during this process will be given by
ACV(T1−T2)BCP(T1−T2)CCP+CV2(T1−T2)D(CP−CV)(T1−T2)One mole of monatomic gas is brought from state A to state B. The initial temperature at A is T0. The temperature at B will be –
 AT0B2T0C3T0D4T0
AT0B2T0C3T0D4T0
A gas is expanded from volume V0 to 2V0 under three different processes, as shown in the figure. Process 1 is isobaric process, process 2 is isothermal and process 3 is adiabatic. Let ΔU1,ΔU2 and ΔU3 be the change in internal energy of the gas in these three processes. Then
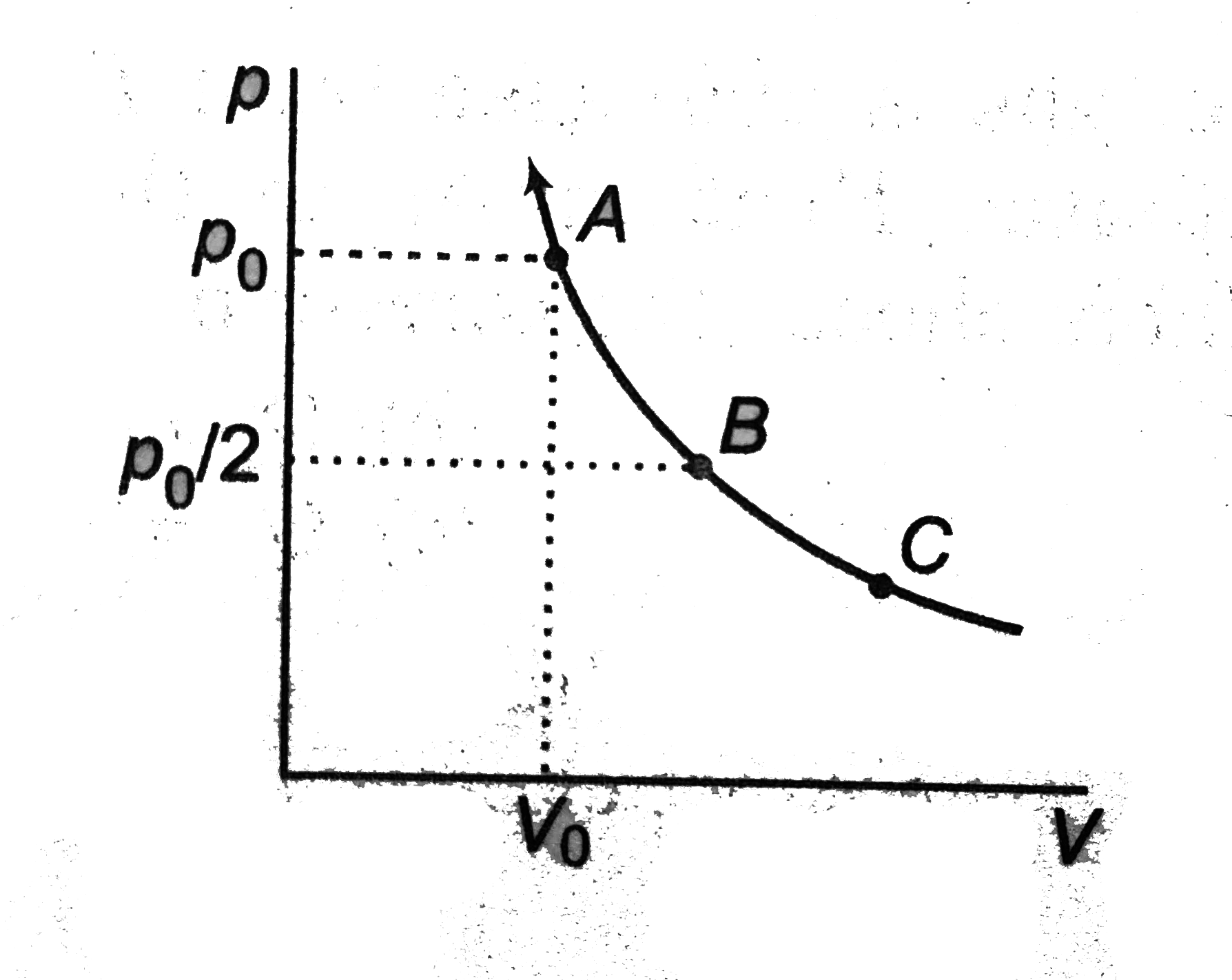
View SolutionThe state of an ideal gas is changed through an isothermal process at temperature T0 as shown in figure. The work done by the gas in going from state B to C is double the work done by gas in going from state A to B. If the pressure in the state B is p02, then the pressure of the gas in state C is
View SolutionA gas is expanded form volume V0→2V0 under three different processes as shown in the figure . Process 1 is isobaric process process 2 is isothermal and and process 3 is adiabatic .
Let ΔU1,ΔU2andΔU3 be the change in internal energy of the gs in these three processes then

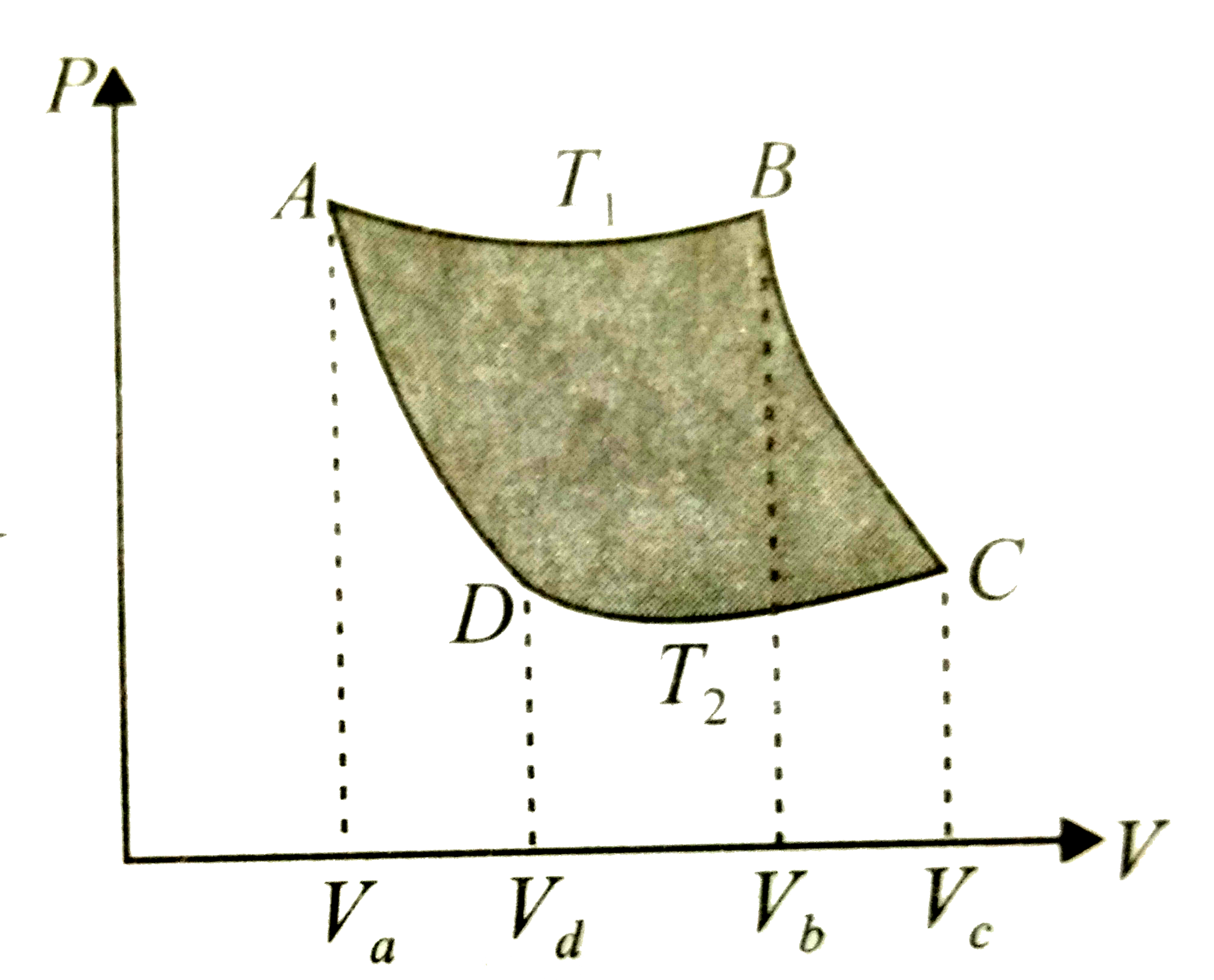
View SolutionTwo different adiabatic parts for the same gas intersect two isothermals at T1andT2 shown in P-V diagram . Then the ratio of VaVb will be
View SolutionFor an ideal gas,
(i) the change in internal energy in a constant pressure process from temperature T1 to T2 is equal to nCV(T2−T1), where CV is the molar heat capacity at constant volume and n is the number of moles of the gas
(ii) The change in internal enregy of the gas and the work done by the gas are equal in magnitude in an adiabatic process.
(iii) The internal energy does not change in an isothermal process. ltbr> (iv) no heat is added or removed in an adiabatic process
View Solution
