The central fringe shifts to the position of fifth bright fringe, if a thin film of refractive index 1.5 is introduced in the path of light of wavelength 5000Å. The thickness of the glass plate is
1μm
5μm
3μm
4μm
The correct Answer is:B
To solve the problem step by step, we will analyze the given information and apply the relevant formulas.
Step 1: Understand the problem
We know that the central fringe shifts to the position of the fifth bright fringe when a thin film of refractive index μ=1.5 is introduced in the path of light with a wavelength λ=5000Å.
Step 2: Identify the formula for fringe shift
The formula for the shift in the position of the fringe due to the introduction of a thin film is given by:
Δy=(μ−1)tλDd
where:
- Δy is the fringe shift,
- μ is the refractive index of the film,
- t is the thickness of the film,
- λ is the wavelength of light,
- D is the distance from the slits to the screen,
- d is the separation between the slits.
Step 3: Set up the equation for the fifth bright fringe
The position of the fifth bright fringe can be expressed as:
y5=5λDd
Since the central fringe shifts to the position of the fifth bright fringe, we can set Δy=y5.
Step 4: Equate the two expressions
From the previous steps, we can equate the expressions:
(μ−1)tλDd=5λDd
Step 5: Simplify the equation
We can cancel λD/d from both sides of the equation:
μ−1=5
Step 6: Solve for thickness t
Substituting μ=1.5:
1.5−1=5⟹0.5t=5
Now, solving for t:
t=50.5=10
Step 7: Substitute the value of λ
Now, substituting λ=5000Å=5000×10−10m=5×10−7m:
t=10×5000Å=10×5000×10−10m=5×10−6m
Step 8: Convert to micrometers
Converting 5×10−6m to micrometers:
t=5μm
Final Answer
The thickness of the glass plate is 5μm.
---
We know that the central fringe shifts to the position of the fifth bright fringe when a thin film of refractive index μ=1.5 is introduced in the path of light with a wavelength λ=5000Å.
The formula for the shift in the position of the fringe due to the introduction of a thin film is given by:
Δy=(μ−1)tλDd
where:
- Δy is the fringe shift,
- μ is the refractive index of the film,
- t is the thickness of the film,
- λ is the wavelength of light,
- D is the distance from the slits to the screen,
- d is the separation between the slits.
The position of the fifth bright fringe can be expressed as:
y5=5λDd
Since the central fringe shifts to the position of the fifth bright fringe, we can set Δy=y5.
From the previous steps, we can equate the expressions:
(μ−1)tλDd=5λDd
We can cancel λD/d from both sides of the equation:
μ−1=5
Substituting μ=1.5:
1.5−1=5⟹0.5t=5
Now, solving for t:
t=50.5=10
Now, substituting λ=5000Å=5000×10−10m=5×10−7m:
t=10×5000Å=10×5000×10−10m=5×10−6m
Converting 5×10−6m to micrometers:
t=5μm
The thickness of the glass plate is 5μm.
Topper's Solved these Questions
Similar Questions
In YDSE, the central bright fringe produced by light of wavelength 5600Å shifts to the position of 5th bright fringe when a thin transparent film of refractive index 1.28 is introduced in the path of light from one of the two slits. Find the thickness of the film.
View SolutionAssuming the expression for the path difference between two interfering light waves for bright and dark fringes, obtain an expression for the fringe width.
The central fringe of a double-slit interference pattern produced by light of wavelength 6000Å shifts to the position of the 5th bright fringe on introducing a thin glass plate of refractive index 1.5 in front of one of the slits. Calculate the thickness of the plate.
View Solution
Knowledge Check
The central fringe of the interference pattern produced by light of wavelength 6000A is found to shift to the position of 4th bright fringe after a glass plate of refraction index 1.5 is introduced in front of one slit in young's experiment. The thickness of the glass plate will be
A4.8μmB8.23μmC14.98μmD3.78μmTo make the central fringe at the centerO , mica sheet of refractive index 1.5 is introduced Choose the corect statement(S).
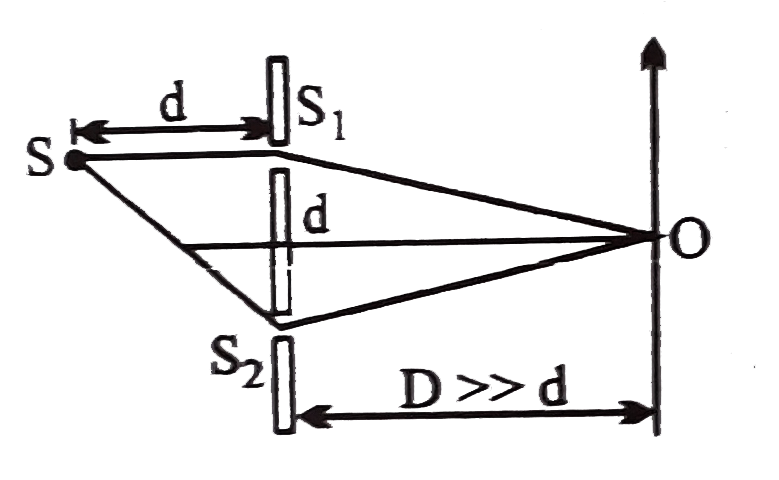 AThe thickness of sheet is 2(√2−1)d infornt of S1BThe thickness of sheet is (√2−1)d infornt of S2CThe thickness of sheet is 2√2d infornt of S1DThe thickness of sheet is (2√2−1)d infornt of S1
AThe thickness of sheet is 2(√2−1)d infornt of S1BThe thickness of sheet is (√2−1)d infornt of S2CThe thickness of sheet is 2√2d infornt of S1DThe thickness of sheet is (2√2−1)d infornt of S1The central fringe of the interference pattern produced by the light of wavelength 6000 Å is found to shift to the position of 4th dark fringe after a glass sheet of refractive index 1.5 is introduced. The thickness of glass sheet would be
A4.8μmB4.2μmC5.4μmD3.0μm
A thin mica sheet of thickness 2×10−6m and refractive index (μ=1.5) is introduced in the path of the first wave. The wavelength of the wave used is 5000Å. The central bright maximum will shift
View SolutionIn YDSE, the sources is red ligth of wavelength 7×10−7m. When a thin glass plate of refractive index 1.5 is put in the path of one of the interfering beams, the central bright fringe shifts by 10−3 m to the position previously occupied by the 5th bright fringe.
If the source is now changed to green light of wavelength 10−7m, the central fringe shifts to a position initially occupied by the sixth bright fringe due to red ligth. What will be refractive index of glass plate for the second ligth for changed source of ligth?
View SolutionA double slit experiment is performed with light of wavelength 500nm. A thin film of thickness 2μm and refractive index 1.5 is introduced in the path of the upper beam. The location of the central maximum will
View SolutionIf a thin transparent plate is introduced, in the path of interfering waves, then entire fringe
View SolutionFringes are produced with monochromatic light of wavelength 5500 Å. A thin glass plate of R.I. 1.5 is then placed normally in one of the paths of interfering beams and the central bright fringe is found to be shifted to the position, previously occupied by the third bright band from the centre. the thickness of the glass plate is
View Solution
