A semicircular wedge of mass M is placed on a horizontal floor. A man of mass m starts moving on wedge from position A with constant speed v relative to the wedge. Initially , both man & wedge were at rest . Neglect the friction between wedge & horizontal surface and man doesn't slips on the wedge while man moves from A to C relative to wedge . The correct statement is

speed of wedge will first increase then decrease
speed of the wedge will remain constant
speed of the wedge first increase up to a maximum value and then remains constant
the wedge doesn't move
The correct Answer is:A
Step by step video & image solution for A semicircular wedge of mass M is placed on a horizontal floor. A man of mass m starts moving on wedge from position A with constant speed v relative to the wedge. Initially , both man & wedge were at rest . Neglect the friction between wedge & horizontal surface and man doesn't slips on the wedge while man moves from A to C relative to wedge . The correct statement is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A wedge of mass m2 is kept on a spring balance. A small block of mass m1 can move along the frictionless incline of the wedge. What is the reading of the balance while the block slides? Ignore the recoil of the wedge.

View Solution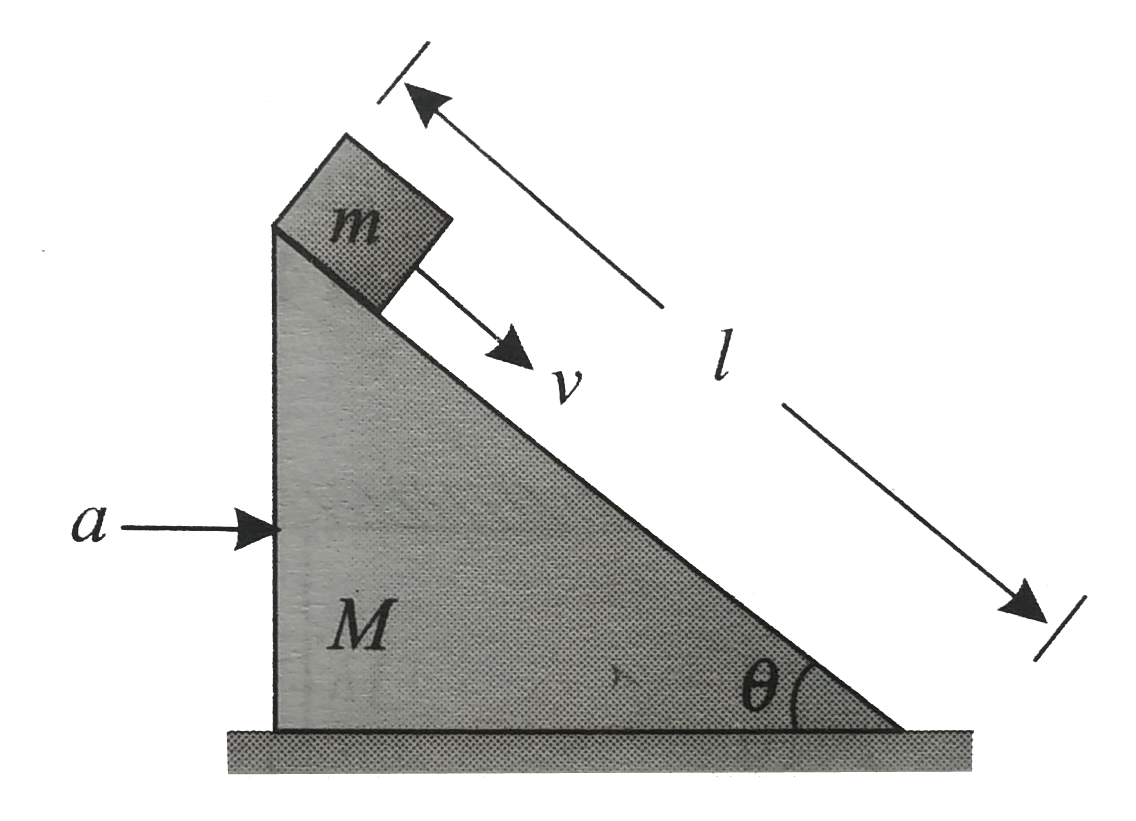
A smooth wedge of mass M is pushed with an acceleration a=>anθ and a block of mass m is projected down the slant with a velocity v relative to the wedge.
Q. The normal reaction between wedge and block is:
View Solution
Knowledge Check
All the surfaces are smooth as shown in figure. The acceleration of mass m relative to wedge is :
 Ag sin θBg sin θ + a cos θCg sin θ - a cos θDa cos θ
Ag sin θBg sin θ + a cos θCg sin θ - a cos θDa cos θ
A smooth wedge of mass M is pushed with an acceleration a=>anθ and a block of mass m is projected down the slant with a velocity v relative to the wedge.
The horizontal force applied on the wedge is:A(M+m)gsinθB(M+m)gcosθCMgsin2θ+MgD(M+m)g+mgcos2θA cube of mass m is placed on top of a wedge of mass 2m, as shown in figure. There is no friction between the cube and the wedge. The minimum co - efficient of friction between the wedge and the horizontal surface, so that the wedge does not move is
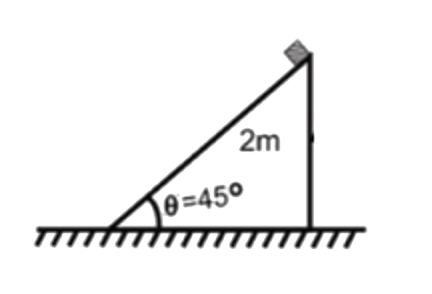 A0.1B0.2C0.3D1√2
A0.1B0.2C0.3D1√2
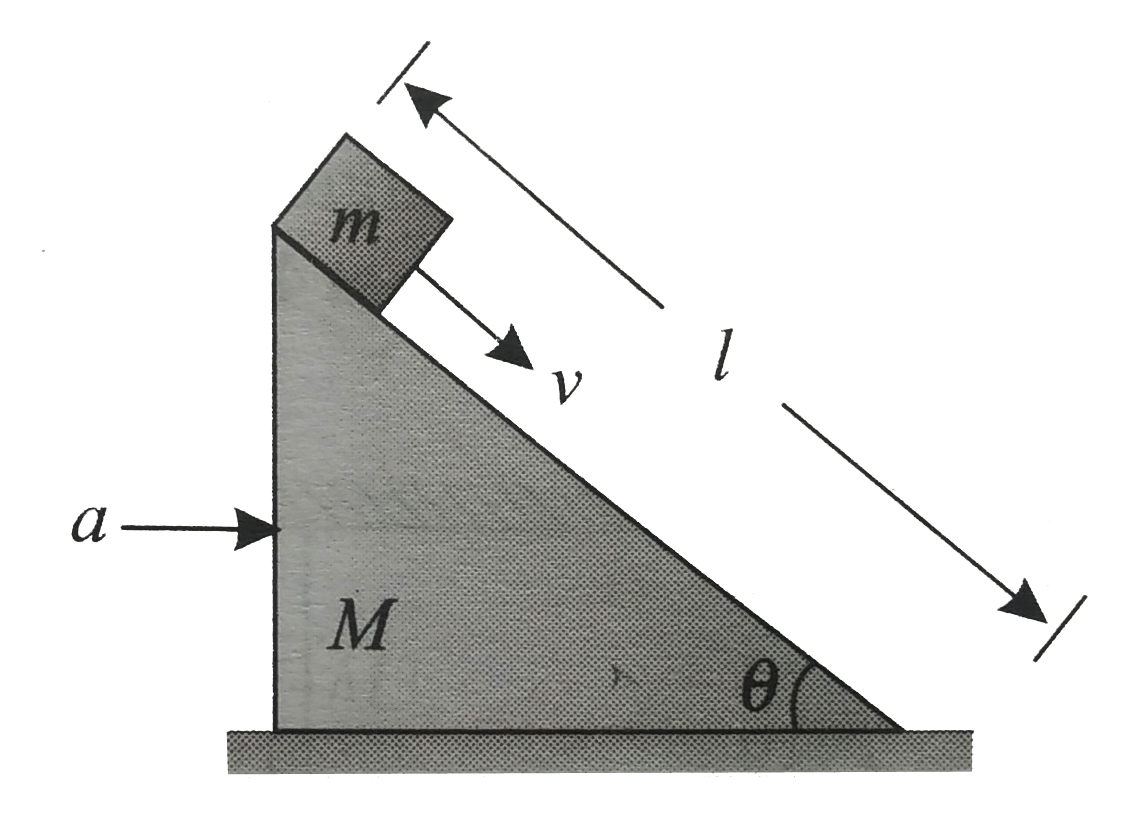
A smooth wedge of mass M is pushed with an acceleration a=>anθ and a block of mass m is projected down the slant with a velocity v relative to the wedge.
Q. The normal reaction offered by ground to the wedge is:
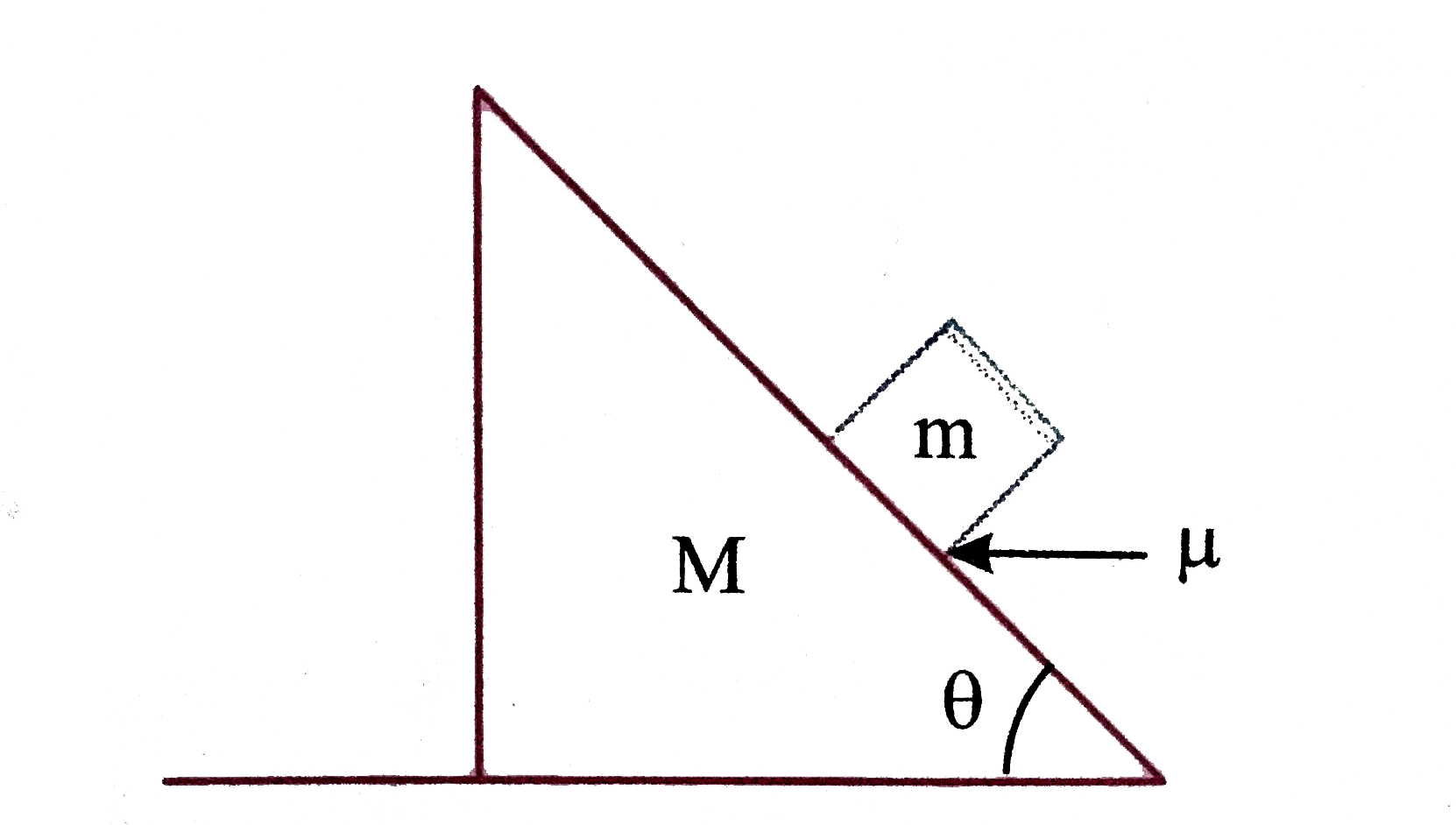
View SolutionCalculate angle of friction between wedge and block system is at rest M coefficient of friction between wedge and block.
View SolutionA block of mass 2 kg is kept on a smooth wedge of mass 3 kg and wedge is kept on a rough horizontal surface. A vertical force of 60 N is applied on the minimum coefficient of friction between the wedge and horizontal surface, so that wedge remains at rest during the motion of block on the wedge ?
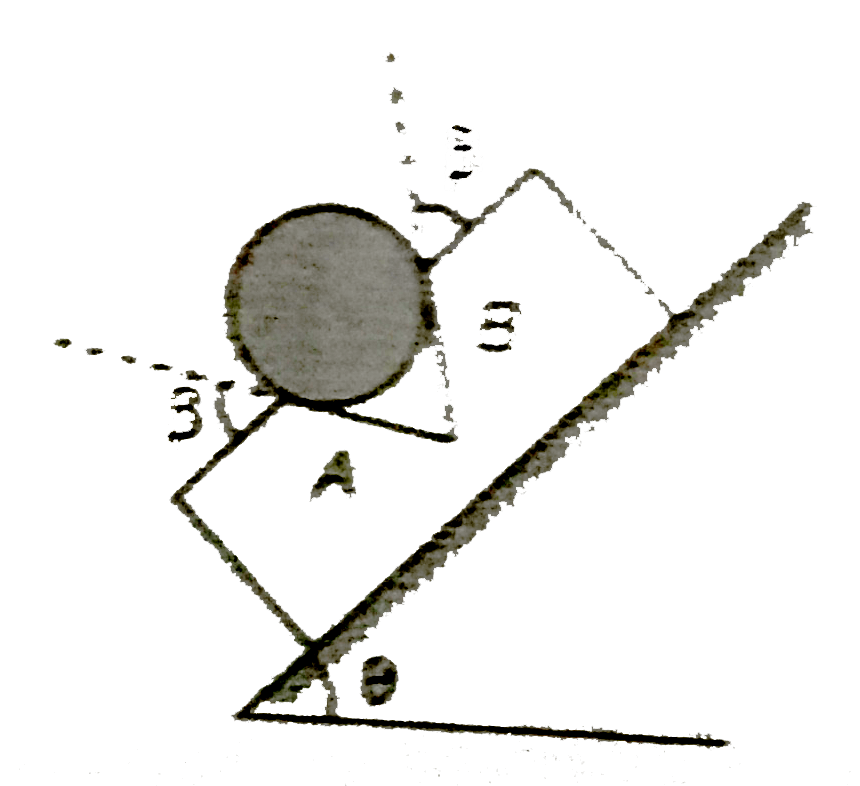
View SolutionA triangular wedge is placed on smooth horizontal surface. A block is placed on wedge as shown in the figure. Coefficient of friction between block and wedge is μ. Initially system reamins at rest.
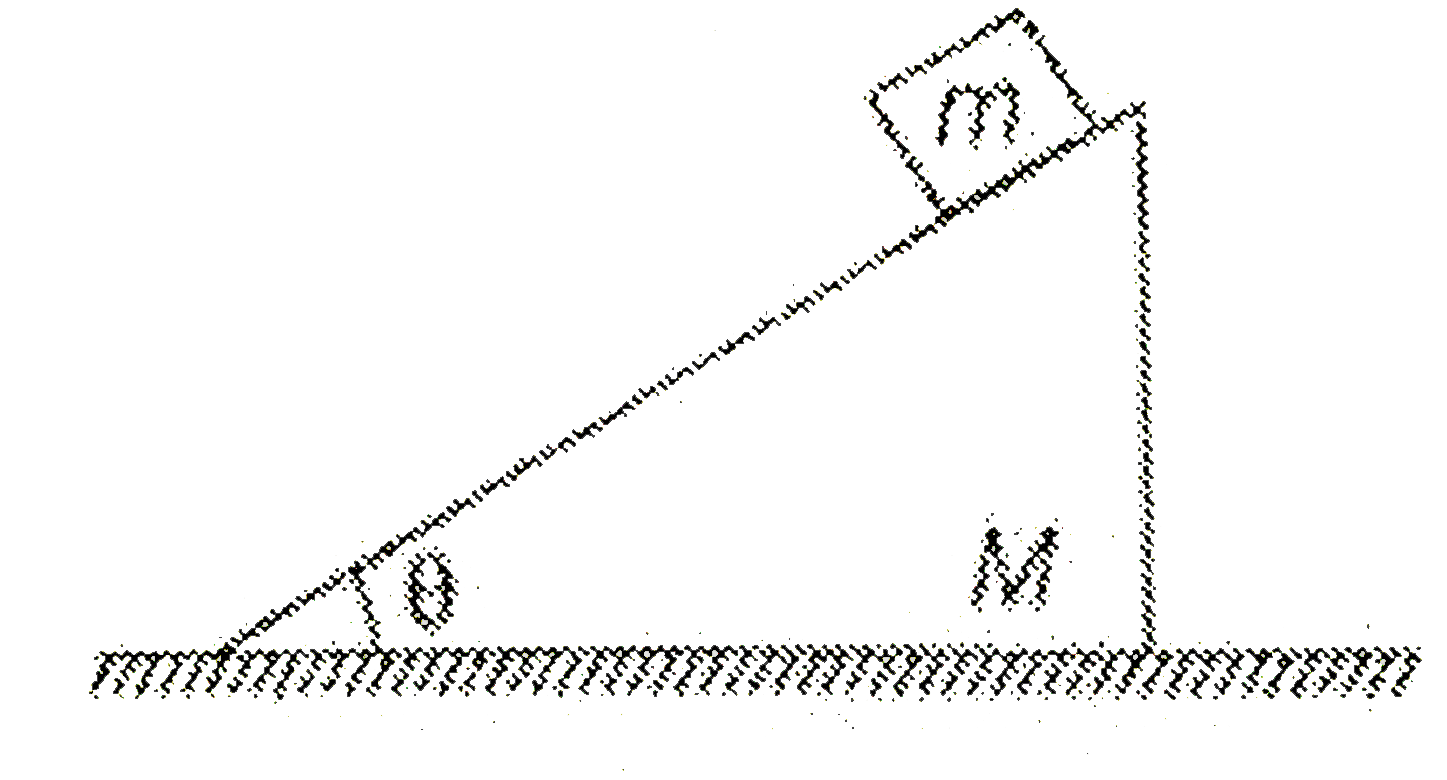
View SolutionA wedge of mass M resting on a horizontal frictionless surface is acted upon by a force F in the horizontal direction as shown in figure. Find the net horizontal force acting on the shaded portion of the wedge.

View Solution
