In the following table ' X " is formed by the division or branching of 'Y ' which one is an exception ?
'X''Y'AArterioleArteryBCapillaryArterioleCVenuleVeinDRenal ArteryAorta
A
B
C
D
The correct Answer is:C
To determine which option is an exception in the relationship between 'X' and 'Y', we need to analyze each pair provided in the table.
1. Understanding the Relationships:
- Arteriole and Artery (Option A): An artery branches into arterioles. This is a standard branching relationship.
- Capillary and Arteriole (Option B): Arterioles branch into capillaries. Again, this follows the expected branching pattern.
- Venule and Vein (Option C): Venules are formed from the convergence of capillaries and then merge to form veins. This is also a typical branching relationship.
- Renal Artery and Aorta (Option D): The aorta branches into various arteries, including the renal artery. However, the renal artery does not branch into the aorta; it is a direct branch from the aorta.
2. Identifying the Exception:
- In options A, B, and C, 'X' is formed by the division or branching of 'Y' as expected.
- In option D, the renal artery does not branch from the aorta; rather, it is a branch of the aorta. Therefore, it does not fit the pattern of 'X' being formed by the division or branching of 'Y'.
3. Conclusion:
- The exception is Option D: Renal Artery and Aorta.
Final Answer:
The exception is Option D: Renal Artery and Aorta.
- Arteriole and Artery (Option A): An artery branches into arterioles. This is a standard branching relationship.
- Capillary and Arteriole (Option B): Arterioles branch into capillaries. Again, this follows the expected branching pattern.
- Venule and Vein (Option C): Venules are formed from the convergence of capillaries and then merge to form veins. This is also a typical branching relationship.
- Renal Artery and Aorta (Option D): The aorta branches into various arteries, including the renal artery. However, the renal artery does not branch into the aorta; it is a direct branch from the aorta.
- In options A, B, and C, 'X' is formed by the division or branching of 'Y' as expected.
- In option D, the renal artery does not branch from the aorta; rather, it is a branch of the aorta. Therefore, it does not fit the pattern of 'X' being formed by the division or branching of 'Y'.
- The exception is Option D: Renal Artery and Aorta.
The exception is Option D: Renal Artery and Aorta.
Topper's Solved these Questions
Similar Questions
Knowledge Check
Students dissected a human kidney longitudinally and drew the given diagram. Choose the correct labelling :
X Y ZACortexMedullaUreterBRenal PyramidBowman's CapsuleRenal ArteryCMedullaCortexUreterDBowman's CapsuleCortexRenal Artery
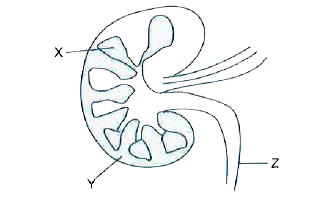 AABBCCDD
AABBCCDDx4+4y4 is divisible by which one of the following ?
A(x2+2xy+2y2)B(x2+2y2)C(x2−2y2)DNone of theseIf b>a,d>c then are of quadrilateral formed by straight lines x=b,x=a,y=candy=d is
A(b−a)(d−c)B12(b−a)(d−c)C(b+a)(d+c)D12(b+a)(d+c)
The following line(s) is (are) tangent to the curve y=x2−x (A) x−y=0 (B) x+y=0 (C) x−y=1 (D) x+y=1
View SolutionLet A={x,y,z}andB={a,b,c,d} . Which one of the following is not a relation from A to B
View Solutionselect the correct option: a. Giomanutus is a a tuft of capillaries formed by the afferent articles which is a fine branch of renal vein b. Giomerulus along with the bowman's capsule forms renal corpuscle c. Vasa recta is a find branch of afferent arteriole which runs parallel to Henie's loop d. in human kidney, cortical nephron and juxtamedullary nephrons are in equal proportion
View SolutionLet A = {x,y,z} and B = {a,b,c,d} Then, which one of the following is not a relation from A to B ?
View SolutionIf A={a,b,c,d}andB={x,y,z}, then which one of the following relations from A to B is not a mapping?
View Solution
