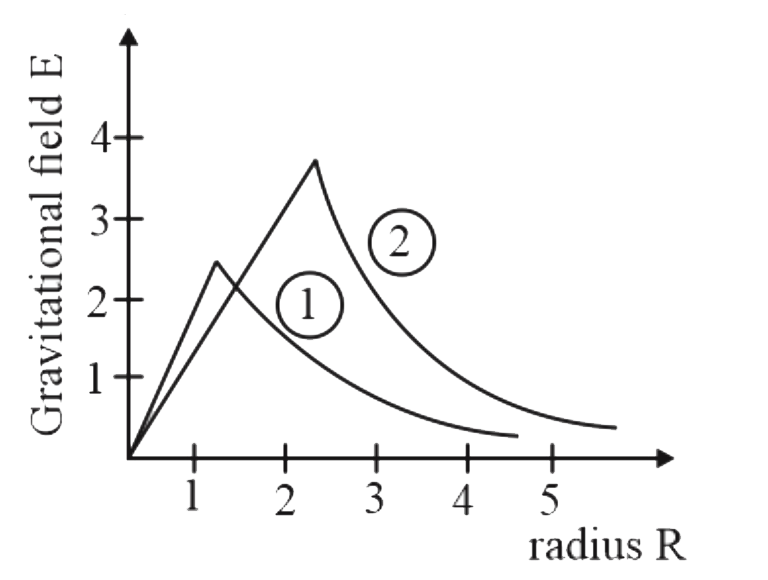
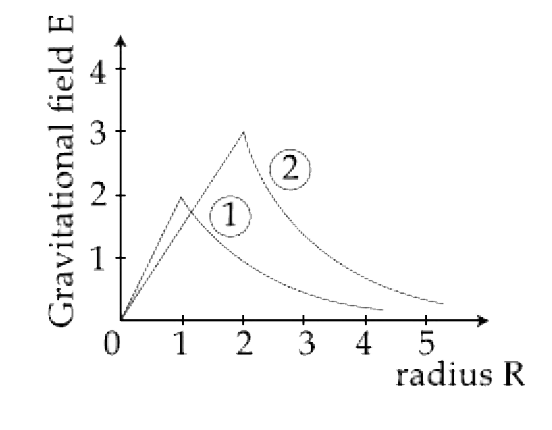
Consider two solid spheres of radii and masses , respectively . The gravitational field due to sphere (1) and (2) are shown. The value of is :
The correct Answer is:B
Step by step video & image solution for Consider two solid spheres of radii R_1 = 1 m, R_2 =2m and masses M_1 and M_2 , respectively . The gravitational field due to sphere (1) and (2) are shown. The value of M_1/M_2 is : by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Consider two solid sphere oFIGURE radii R1=1m,R2=2m and masses M1andM2, respectively. The gravitional FIGUREield due to sphere 1 and 2 are shown. The value oFIGURE M1M2) is:
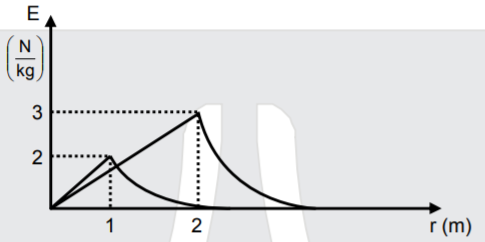
View SolutionTwo spherical bodies of mass m1 & m2 are having radius 1 m & 2 m respectively. The gravitational field of the two bodies with their radial distance is shown below. The value of m1m2 is
 -
-
View Solution
Knowledge Check
The figure represents two concentric shells of radii R1 and R2 and masses M1 and M2 respectively. The gravitational field intensity at the point A at distance a(R1<a<R2) is
 AG(M1+M2)a2BGM1a2+GM2R22CGM1a2Dzero
AG(M1+M2)a2BGM1a2+GM2R22CGM1a2DzeroThe slope of graph as shown in figure at points 1, 2 and 3 is m1,m2andm3 respectively then
 Am1>m2>m3Bm1<m2<m3Cm1=m2=m3Dm1=m3>m2
Am1>m2>m3Bm1<m2<m3Cm1=m2=m3Dm1=m3>m2Two bodies of masses M1 and M2, are placed at a distance R apart. Then at the position where the gravitational field due to them is zero, the gravitational potential is
A−G√M1RB−G√M2RC−(√M1+√M2)2GRD−(√M1−√M2)2GR
Two bodies of masses m1andm2(<m1) are connected to the ends of a massless cord and allowed to move as shown in figure. The pulley is both massless and frictionless. The acceleration of the centre of mass is (m1−m2)n(m1+m2)2g. Find the value of n.

View SolutionTwo concentric spherical shells of masses and radii m1,r1andm2,r2 respectively are as shown. The gravitational field intensity at point P is

View SolutionFrom a solid sphere of mass M and radius R, a solid sphere of radius R/2 is removed as shown. Find gravitational force on mass m as shown

View SolutionTwo concentric shells of masses M1 and M2 are concentric as shown. Calculate the gravitational force on m due to M1 at points P,Q and R.

View SolutionParticles of masses m1 and m2 are at a fixed distance apart. If the gravitational field strength at m1 and m2 are →I1 and →I2 respectively. Then,
View Solution
