The figure shows a region containing a uniform magnetic field B, which is increasing at the rate dBdt The region is gravity free. A disc of mass m and radius R is kept in this magnetic field. Two charged particles having charge q1andq2 and masses m and 2m are embedded to the non-conducting disc on the circumference at diametrically opposite points. The disc is free to translate as well as rotate.

If q1=−qandq2=q , then the initial acceleration of q1 will be
qR3mdBdt
2qR3mdBdt
2qRmdBdt
qRmdBdt
The correct Answer is:A
Step by step video & image solution for The figure shows a region containing a uniform magnetic field B, which is increasing at the rate (dB)/(dt) The region is gravity free. A disc of mass m and radius R is kept in this magnetic field. Two charged particles having charge q_1 and q_2 and masses m and 2m are embedded to the non-conducting disc on the circumference at diametrically opposite points. The disc is free to translate as well as rotate. If q_1 = -q and q_2 = q , then the initial acceleration of q_1 will be by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A charged particle having charge q is moving in a uniform magnetic field B parallel to the lines of field force, the magnetic force acting on a charge will be qvB
View SolutionThe figure shows two regions of uniform magnetic field of strengths 2B and 2B. A charged particle of mass m and charge q enters the region of the magnetic field with a velocity υ=qBwm, where w is the width of each region of the magnetic field. The time taken by the particle to come out of the region of the magnetic field is
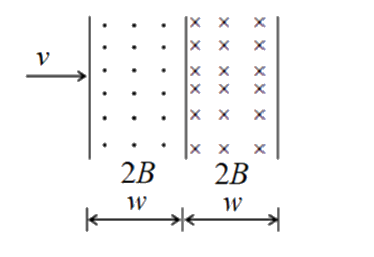
View Solution
Knowledge Check
Two charged particles of charge +2q and +q have masses m and 2m respectively. Then are kept in uniform electric field allowed to move for the same time. Find the ratio of their kinetic energies.
A1:8B16:1C2:1D3:1A circular disc of mass M and radius R is rotating with angular velocity ω . If two small spheres each of mass m are gently attached to two diametrically opposite points on the edge of the disc, then the new angular velocity of the disc will be
A(M+4mM)ωB(MM+4m)ωC(M+mM)ωD(MM+2m)ωA charged particle of charge q and mass m is shot into a uniform magnetic field of induction B at an angle θ with the field. The frequency of revolution of the particle
ADepends on the angle θBIs independent of the angle θCIs proportional to the specific charge q/m of the particleDIs inversely proportional to the value of B
A disc of mass m and radius R is kept on a smooth horizontal surface with its plane parallel to the surface. A particle of same mass m travelling with speed v0 collides with the stationery disc and gets embedded into it as shown in the figure. Then

View SolutionCalculate gravitational field intensity at a distance x on the axis from centre of a uniform disc of mass M and radius R .
View SolutionA positive charge particle of charge q, mass m enters into a uniform magnetic field with velocity v as shown in the figure. There is no magnetic field to the left of PQ. Find

distance travelled in the magnetic field
View SolutionA positive charge particle of charge q, mass m enters into a uniform magnetic field with velocity v as shown in the figure. There is no magnetic field to the left of PQ. Find
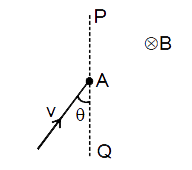
impulse of magnetic force.
View SolutionThe magnetic field is confirmed in a square region. A positive charged particle of charge q and mass m the limiting velocities of the particles so that it may come out of face (1), (2), (3), and (4).

View Solution
