A short linear object of length b lies on the axis of a concave mirror of focal length F at a distance u from the pole. The length of the image will be
(fu−f)b
(u−ff)b
(fu−f)2b
(u−ff)2b
The correct Answer is:C
To find the length of the image of a short linear object of length b placed at a distance u from the pole of a concave mirror with focal length F, we can follow these steps:
1. Understand the Setup:
- We have a concave mirror with a focal length F.
- The object is placed at a distance u from the mirror's pole.
- The object has a length b.
2. Use the Mirror Formula:
- The mirror formula is given by:
1v+1u=1F
- Here, for a concave mirror, the focal length F is considered negative. Thus, we can rewrite the equation as:
1v+1(−u)=1(−F)
3. Rearranging the Mirror Formula:
- Rearranging the formula gives:
1v=1u−1F
- This can be simplified to:
v=uFu−F
4. Determine the Magnification:
- The magnification m produced by the mirror is given by:
m=−vu
- Substituting the value of v:
m=−uFu−Fu=−Fu−F
5. Calculate the Length of the Image:
- The length of the image b′ can be calculated using the magnification:
b′=m⋅b=−Fu−F⋅b
- Since we are interested in the magnitude of the image length, we take the absolute value:
|b′|=Fu−F⋅b
Final Result:
The length of the image is given by:
|b′|=F⋅bu−F
- We have a concave mirror with a focal length F.
- The object is placed at a distance u from the mirror's pole.
- The object has a length b.
- The mirror formula is given by:
1v+1u=1F
- Here, for a concave mirror, the focal length F is considered negative. Thus, we can rewrite the equation as:
1v+1(−u)=1(−F)
- Rearranging the formula gives:
1v=1u−1F
- This can be simplified to:
v=uFu−F
- The magnification m produced by the mirror is given by:
m=−vu
- Substituting the value of v:
m=−uFu−Fu=−Fu−F
- The length of the image b′ can be calculated using the magnification:
b′=m⋅b=−Fu−F⋅b
- Since we are interested in the magnitude of the image length, we take the absolute value:
|b′|=Fu−F⋅b
The length of the image is given by:
|b′|=F⋅bu−F
Topper's Solved these Questions
Similar Questions
(a) A short linear object of length b lies along the axis of a concave mirror of focal length f at a distance u from the pole. What is the size of the image? (b) If the object begins to move with speed V0 , what will be the speed of its image?
View SolutionA short linear object of length / lies along the axis of a concave mirror of focal length f at a distance d from the pole of the mirror. The approximate size of the image is
View Solution
Knowledge Check
A short linear object of length b lies along the axis of a concave mirror or focal length f at a distance u from the pole of the mirror. The size of the image is approximately equal to
Ab(u−ff)12Bb(fu−f)12Cb(u−f2)Db(fu−f)2What is the size of the image when a short linear object of length b lies along the axis of a concave mirror of focal length f at a distance u from the pole.
Ab[fμ−f]2Bf[fμ−f]2Cμ[fu−f]2D(ff−u)2A short linear object of length b lies along the axis of a concave mirror of focal length f at a distanee u from the pole of the mirror. The size of the image is approximately equal to
Ab(u−ff)12Bb(fu−f)12Cb(u−ff)Db(fu−f)2
A short linear object of length l lies on the axis of a spherical mirror of focal length f, at a distance x from the mirror. Then, the length of the image (P) so obtained will be

View SolutionA short linear object of length b lies along the axis of a concave mirror or focal length f at a distance u from the pole of the mirror. The size of the image is approximately equal to
View SolutionA short linear object of length / lies along normal to the axis of a concave mirror of focal length f at a distance d from the pole of the mirror. The size of the image is then (nearly)

View SolutionA short linear object of length l lies on the asix of a spherical mirror of focal length f, at a distance x from the mirror. Then, the length of the image (P) so obtained will be
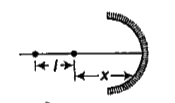
View SolutionAn object of length 6 cm is placed on the principle axis of a concave mirror of focal length f at a distance of 4 f . The length of the image will be
View Solution
