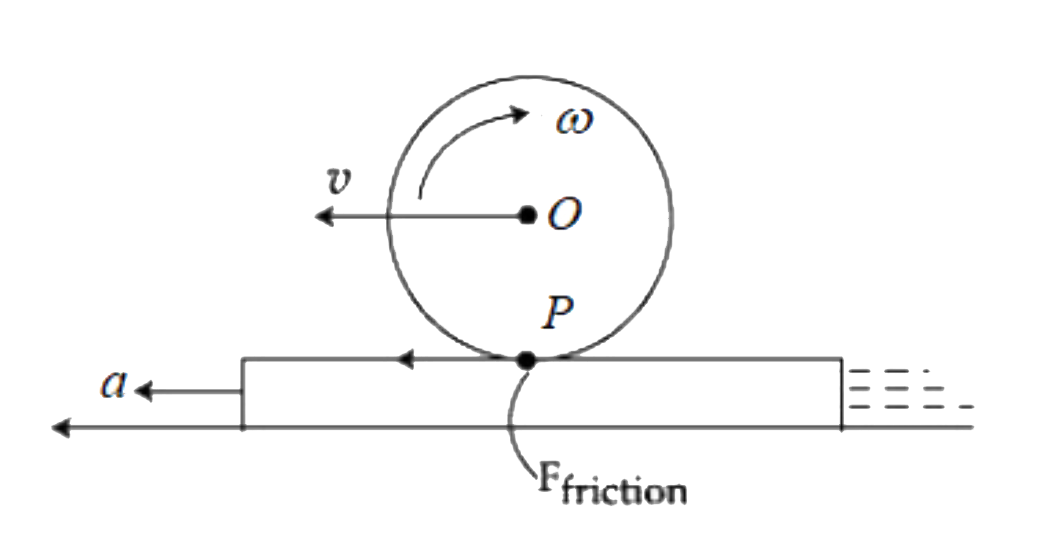
Consider a cylinder of mass M resting on a rough horizontal rug that i

The moment of inertia of a solid cylinder of mass M, length 2R and radius R about an axis passing through the centre of mass and perpendicular to the axis of the cylinder is $I_{1}$ and about an axis passing through one end of the cylinder and perpendicular to the axis of cylinder is $I_{2}$
A $l_{2} - l_{1} = M R^{2}$
B $l_{2} = l_{1}$
C $\frac{l_{2}}{l_{1}} = \frac{19}{12}$
D $l_{1} - l_{2} = M R^{2}$
The moment of inertia of a solid cylinder of mass M, length 2 R and radius R about an axis passing through the centre of mass and perpendicular to the axis of the cylinder is I, and about an axis passing through one end of the cylinder and perpendicular to the axis of cylinder is $I_{2}$ then
A $I_{2} > I_{1}$
B $I_{2} - I_{1} = M R^{2}$
C $\frac{I_{2}}{I_{1}} = \frac{19}{12}$
D $\frac{I_{2}}{I_{1}} = \frac{7}{6}$
A uniform solid cylinder of mass $m$ and radius $R$ is placed on a rough horizontal surface. A horizontal constant force $F$ is applied at the top point P of the cylinder so that it start pure rolling. The acceleration of the cylinder is
A $F / 3 m$
B $2 F / 3 m$
C $4 F / 3 m$
D $5 F / 3 m$

Consider a cylinder of mass M resting on a rough horizontal rug that is pulled out from under it with acceleration 'a' perpendicular to the axis of the cylinder. What is $F_{friction}$ at point P ? It is assumed that the cylinder does not slip.