The volume of brick is 2.197L. The submerged brick is balanced by a 2.54 kg mass on the beam scale. The weight of the brick is
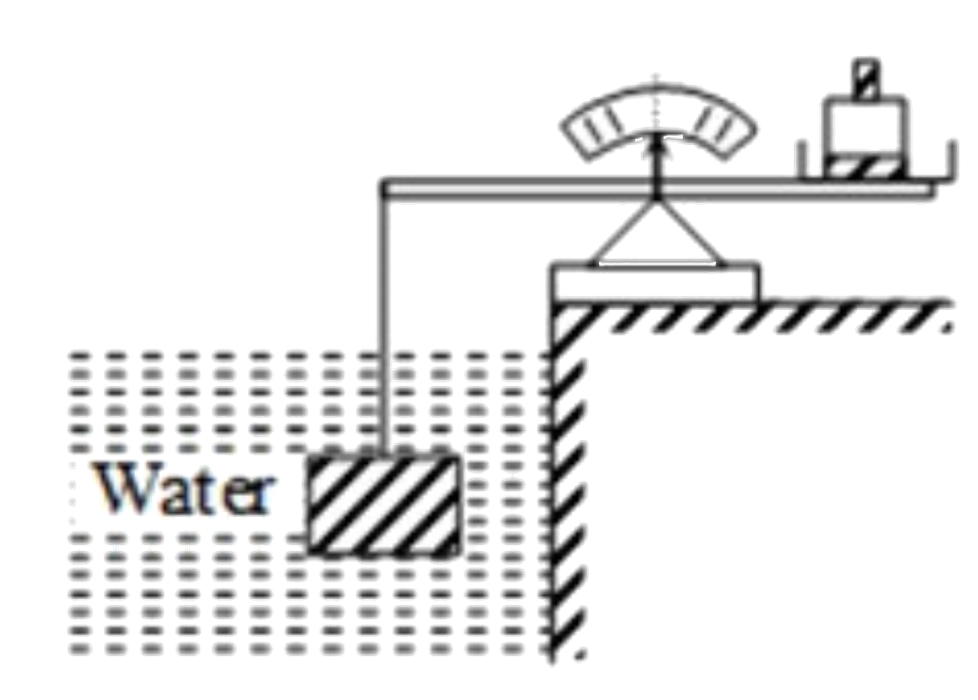
46 N
50 N
56 N
72 N
The correct Answer is:A
Step by step video & image solution for The volume of brick is 2.197L. The submerged brick is balanced by a 2.54 kg mass on the beam scale. The weight of the brick is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The wire of a Young's modules appartus is elongated by 2 mm when a brick is suspended from .it When the brick is immersed in water the wire contracts by 0.6mm Calculate the density of the brick given that the density of water is 1000kgm−3
View SolutionCalculate the pressure exerted by a brick, which applies a force of 2.5 N, when (a) it is placed upright on the soil, (b) when it is placed on its widest base. The dimensions of the brick are 25cm×10cm×5cm
View Solution
Knowledge Check
In figure, block A hangs by a cord form spring balance D and it submerged in a liquid C contained in a beaker B. The mass of the beaker is 1kg. The mass of the liquid is 1.5kg. Balance D reads 7.5kg. The volume of block A is 0.003m3. The mass per unit volume of the liquid is
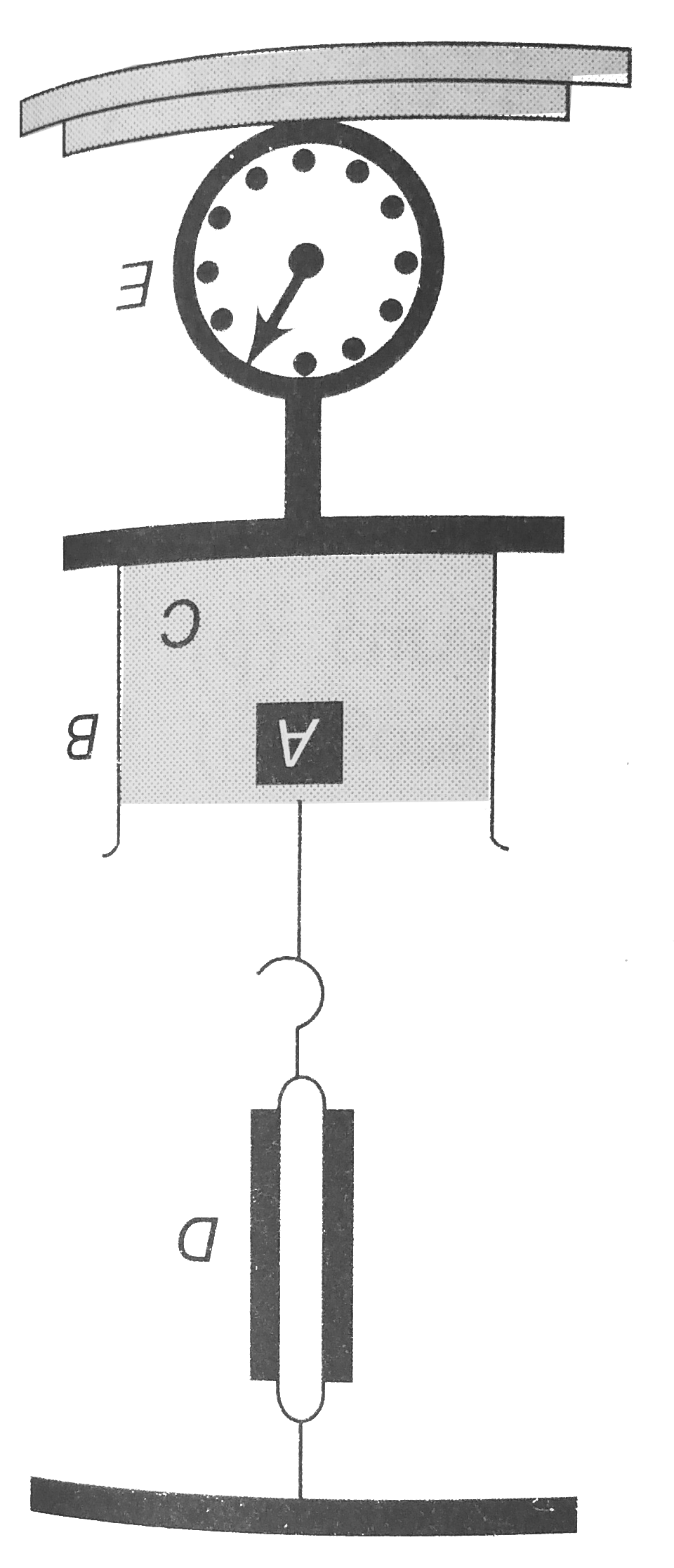 A2500kgm−3B5000kgm−3C1kgm−3D50003kgm−3
A2500kgm−3B5000kgm−3C1kgm−3D50003kgm−3If 716 of the weight of a brick is 218 kg, then 512 of the weight of the brick will be :
A103kgB35 kgC310 kgD52 kgPASSAGE-II : Two bricks each of same dimensions are placed on level ground. Surface area of end of each brick is 40cm2 and the surface area of base of each brick is 150cm2. Each brick weighs 40 N.
If both bricks are placed on standing position then, the total pressure exerted by the bricks on ground is:A100Nm−2B200Nm−2C300Nm−2D400Nm−2
A balance similar to a Roman steel yard is constructed such that the length of the scale on the beam of the balance is 50 cm and the least count on the scale is 1 mm. The zero mark of the scale is at a distance of 15 cm from the point of suspension of the balance. The hook that is used to attach the loads and the centre of gravity of the beam are at distance 8 cm and 5 cm, respectively, from its fulcrum. If the weight of the rider of the balance is 50 gf, find the weight of the beam, the maximum load that can be measured using the balance and its least count.
View SolutionCase 1: If you take a spring balance and a brick. Tie the spring balance with the brick, as shown in figure below. Now, pull the brick with some force and observe it.
Case 2: Wrap a butter paper or a polythene bag around the brick. Now, pul the brick again and check the difference.

What will you observe when brick was pulled by spring balance.
View SolutionCase 1: If you take a spring balance and a brick. Tie the spring balance with the brick, as shown in figure below. Now, pull the brick with some force and observe it.
Case 2: Wrap a butter paper or a polythene bag around the brick. Now, pul the brick again and check the difference.

If you wrap brick with the polythene bag will you observe any difference.
View SolutionIn Fig, a lead brick rests horizontally on cylinders A and B. The areas of the top faces of the cylinders are related by AA=2.2AB, the Young's moduli of the cylinders are related by EA=2.2EB. The cyclinders had identical lengths before the brick was placed on them. What fraction of the brick's mass is supported (a) by cylinder A and (b) by cylinder B ? The horizontal distances between the center of mass of the brick and the centerlines of the cylinders are dA for cylinder A and dB for cylinder B. (c ) What is the ratio dA/dB ?

View SolutionStatement I: Imagine holding two identical bricks under water. Brick A is completely submerged just below the surface of water, while brick B is at a greater depth. The magnitude of force exerted by the person (on the brick) to hold brick B in place is the same as magnitude of force. exerted by the person (on the brick) to hold brick A in place.
Statement II: The magnitude of buoyant force on a brick completely submerged in water is equal to the magnitude of weight of water it displaced and does not depend on the depth of the brick in water.
View Solution
