Oxygen atom forms FCC unit cell with 'A ' atoms occupying all tetrahedral voids and 'B ' atoms occupying all octahedral voids. If atoms are removed from two of the body diagonals then determine the formula of resultant compound formed .
A4B4O7
A8B6O7
A8B8O7
A6B8O6
The correct Answer is:B
To solve the problem, we need to analyze the structure of the FCC unit cell and the distribution of atoms in the tetrahedral and octahedral voids, as well as the effect of removing atoms from the body diagonals.
1. Understanding the FCC Structure:
- In a Face-Centered Cubic (FCC) unit cell, oxygen (O) atoms are located at the corners and face centers of the cube.
- There are 8 corner atoms (each contributes 1/8) and 6 face-centered atoms (each contributes 1/2).
- Total contribution of O atoms = 8×18+6×12=1+3=4 O atoms per unit cell.
2. Identifying Tetrahedral and Octahedral Voids:
- In an FCC structure, there are 8 tetrahedral voids and 4 octahedral voids.
- Tetrahedral voids are located at positions that are 14,14,14 and its equivalents.
- Octahedral voids are located at the center of the cube and at the midpoints of the edges.
3. Filling the Voids:
- 'A' atoms occupy all tetrahedral voids. Since there are 8 tetrahedral voids, there will be 8 A atoms.
- 'B' atoms occupy all octahedral voids. Since there are 4 octahedral voids, there will be 4 B atoms.
4. Removing Atoms from Body Diagonals:
- The body diagonal of the cube connects opposite corners. Each body diagonal contains 2 tetrahedral voids.
- If we remove atoms from 2 body diagonals, we are effectively removing 4 A atoms (2 from each diagonal).
- After removing these, the number of A atoms left = 8−4=4.
5. Counting Remaining Atoms:
- The number of B atoms remains unchanged at 4 since we are not removing any B atoms.
- The number of O atoms remains unchanged at 4.
6. Determining the Formula:
- After the removal of atoms, we have:
- A = 4
- B = 4
- O = 4
- Therefore, the formula of the resultant compound can be expressed as A4B4O4.
- This can be simplified to A4B4O4 or A1B1O1 if we divide by 4.
Final Result:
The formula of the resultant compound formed is A4B4O4.
---
- In a Face-Centered Cubic (FCC) unit cell, oxygen (O) atoms are located at the corners and face centers of the cube.
- There are 8 corner atoms (each contributes 1/8) and 6 face-centered atoms (each contributes 1/2).
- Total contribution of O atoms = 8×18+6×12=1+3=4 O atoms per unit cell.
- In an FCC structure, there are 8 tetrahedral voids and 4 octahedral voids.
- Tetrahedral voids are located at positions that are 14,14,14 and its equivalents.
- Octahedral voids are located at the center of the cube and at the midpoints of the edges.
- 'A' atoms occupy all tetrahedral voids. Since there are 8 tetrahedral voids, there will be 8 A atoms.
- 'B' atoms occupy all octahedral voids. Since there are 4 octahedral voids, there will be 4 B atoms.
- The body diagonal of the cube connects opposite corners. Each body diagonal contains 2 tetrahedral voids.
- If we remove atoms from 2 body diagonals, we are effectively removing 4 A atoms (2 from each diagonal).
- After removing these, the number of A atoms left = 8−4=4.
- The number of B atoms remains unchanged at 4 since we are not removing any B atoms.
- The number of O atoms remains unchanged at 4.
- After the removal of atoms, we have:
- A = 4
- B = 4
- O = 4
- Therefore, the formula of the resultant compound can be expressed as A4B4O4.
- This can be simplified to A4B4O4 or A1B1O1 if we divide by 4.
The formula of the resultant compound formed is A4B4O4.
Topper's Solved these Questions
Similar Questions
A forms ccp lattice B occupy half of the octahedral voids and O occupy all the tetrahedral voids. Calculate formula-
View SolutionIn a hypothetical solid, C atoms are found to form cubical close-packed lattice. A atoms occupy all tetrahedral voids and B atoms occupy all octahedrals voids.

A and B atoms are of appropriate size, so that there is no distortion in the p lattice of C atoms. Now if a plane as shown in the following figure is cut, then the cross section of this plane will look like
View Solution
Knowledge Check
In a hypothetical solid C atoms form C C P lattice with A atoms occupying all the Tetrahedral Voids and B atoms occupying all the octahedral voids A and B atoms are of the appropriate size such that there is no distortions in the CCP lattice. Now if a plane is cut ( as shown ) then the section would like
 A
A B
B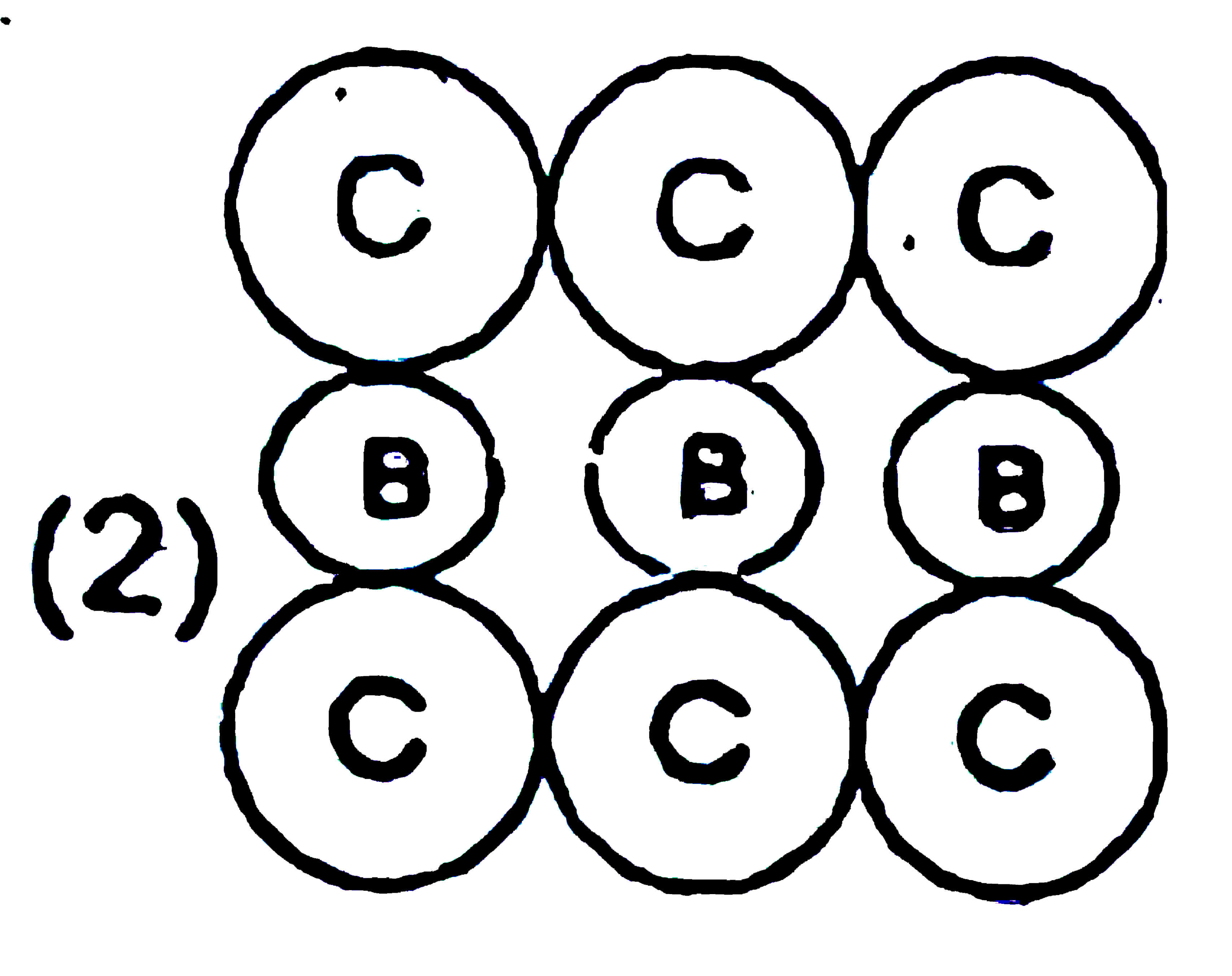 C
C D
D
In a ccp structure of X atoms, Y atoms occupy all the octahedral holes. If 2X atom are removed from corners and replaced by Z, then the formula of the compound will be
AX15Y16ZBX7Y8ZCX7.5Y8ZDX8Y8Z3In fcc , a tetrahedral void is formed by atoms at
A3 corners and 1 face centreB3 face centres and 1 cornerC2 face centres and 2 cornersD2 face centres , 1 corner and 1 body centre
In a hypothetical solid , C atoms are found to form cubical close - packed lattice . A atoms occupy all tetrahedral voids and B atoms occupy all octahedral voids .
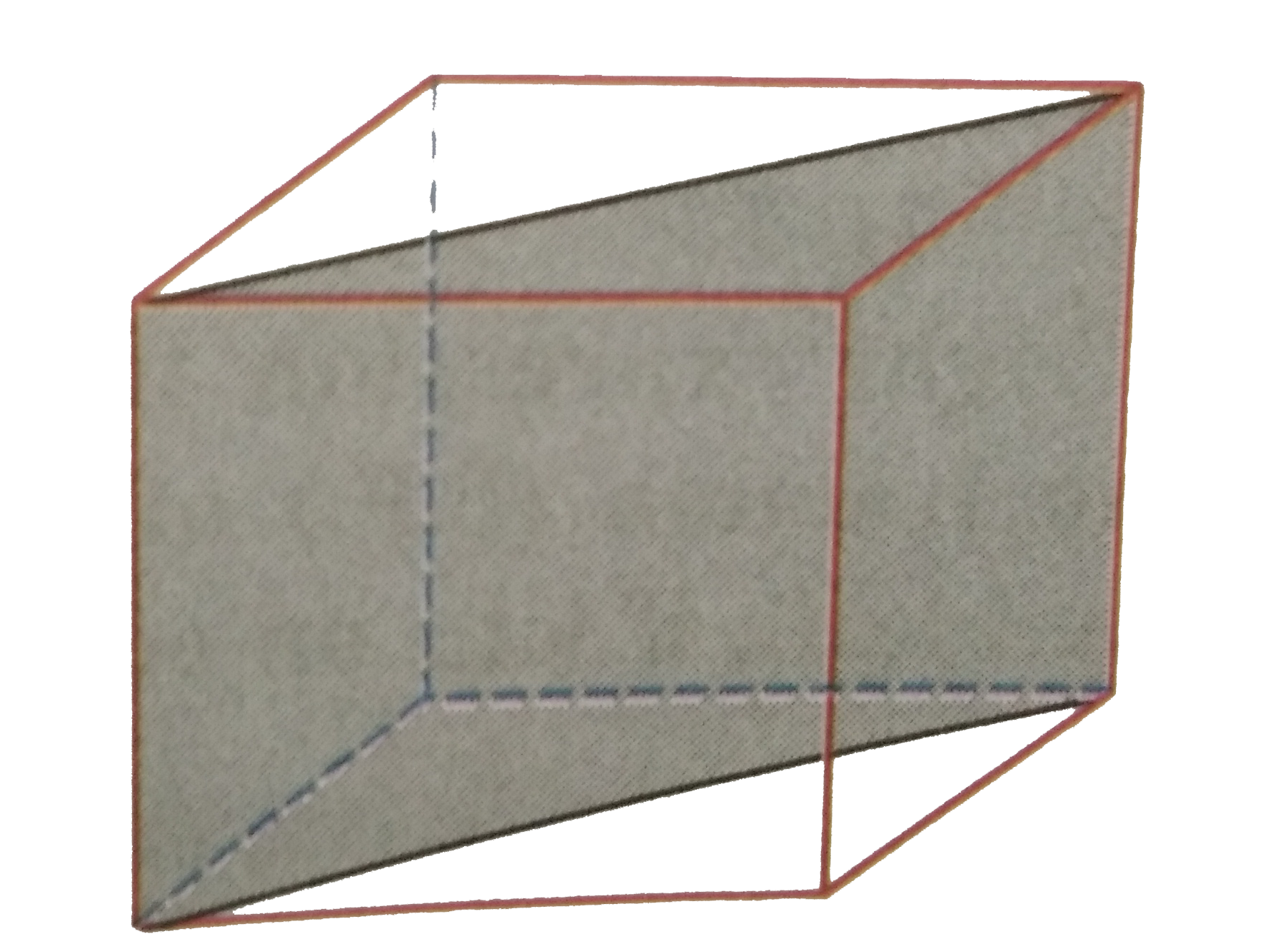
A and B atoms are of appropriate size , so that there is no distortion in the ccp lattice of C atoms . Now if a plane as shown in the above figure is cut , then the cross section of this plane will look like
View SolutionA solid is formed by three elements X,Y and Z, X atoms form a fcc lattice with Y atoms occupying all tetrahedral voids. Z atoms occupying half the octahedral voids. The formula of the solids is :
View SolutionAtoms A present in ccp lattice atoms B occupied tetrahedral voids and atoms C present in octahderal voids. The formula of compound is
View SolutionA crystal is made of particle X,Y and Z 'X' forms +FCC packing+. 'Y' occupies all the octahedral voids of X and Z occupies all tetrahedral voiods of X. If all the particles along one body diagonal are removed, then the formula of the crystal would be?
View SolutionIn a structure, A atoms have fcc arrangement B atoms occupy all the tetrahedral sites and C atoms occupy half the octahedral sites. The formula of the compound is
View Solution
