A body is thrown from a point with speed 50ms−1 at an angle 37∘ with horizontal . When it has moved a horizontal distance of 80 m then its distance from point of projection is
40 m
40√2m
40√5m
none
The correct Answer is:C
To solve the problem step by step, we will break it down into manageable parts:
Step 1: Determine the horizontal and vertical components of the initial velocity.
The body is thrown with an initial speed v=50m/s at an angle θ=37∘.
- Horizontal Component (vx):
vx=v⋅cos(θ)=50⋅cos(37∘)
Using cos(37∘)≈45:
vx=50⋅45=40m/s
- Vertical Component (vy):
vy=v⋅sin(θ)=50⋅sin(37∘)
Using sin(37∘)≈35:
vy=50⋅35=30m/s
Step 2: Calculate the time taken to travel a horizontal distance of 80 m.
The horizontal motion is uniform, so the time t taken to cover the horizontal distance x=80m is given by:
t=xvx=8040=2s
Step 3: Calculate the vertical displacement after 2 seconds.
Using the formula for vertical displacement sy:
sy=vy⋅t+12(−g)t2
where g≈10m/s2 (acceleration due to gravity).
Substituting the values:
sy=30⋅2+12(−10)(22)
sy=60−20=40m
Step 4: Calculate the distance from the point of projection.
Now, we need to find the resultant distance d from the point of projection using the Pythagorean theorem:
d=√x2+s2y
Substituting x=80m and sy=40m:
d=√802+402=√6400+1600=√8000=40√5m
Final Result
The distance from the point of projection is:
d≈89.44m
The body is thrown with an initial speed v=50m/s at an angle θ=37∘.
vx=v⋅cos(θ)=50⋅cos(37∘)
Using cos(37∘)≈45:
vx=50⋅45=40m/s
vy=v⋅sin(θ)=50⋅sin(37∘)
Using sin(37∘)≈35:
vy=50⋅35=30m/s
The horizontal motion is uniform, so the time t taken to cover the horizontal distance x=80m is given by:
t=xvx=8040=2s
Using the formula for vertical displacement sy:
sy=vy⋅t+12(−g)t2
where g≈10m/s2 (acceleration due to gravity).
sy=30⋅2+12(−10)(22)
sy=60−20=40m
Now, we need to find the resultant distance d from the point of projection using the Pythagorean theorem:
d=√x2+s2y
Substituting x=80m and sy=40m:
d=√802+402=√6400+1600=√8000=40√5m
The distance from the point of projection is:
d≈89.44m
Topper's Solved these Questions
Similar Questions
A ball is projected from ground with a speed of 20ms−1 at an angle of 45∘ with horizontal.There is a wall of 25m height at a distance of 10m from the projection point. The ball will hit the wall at a height of
View SolutionA ball projected from the ground with speed 10m/s at an angle of 45∘ with horizontal. It collides with a wall at a distance 2 m from the point of projection and returns to its original position. If the coefficient of restitution between the ball and wall is 1/x, find x.
View Solution
Knowledge Check
A stone is projected with speed of 50ms−1 at an angle of 60∘ with the horizontal. The speed of the stone at highest point of trajectory is
A75ms−1B25ms−1C50ms−1Dcannot findA projectile is fired at an angle of 45∘ with the horizontal. Elevation angle of the projection at its highest point as seen from the point of projection is
A60∘Btan−1(12)Ctan−1(√32)D45∘A ball is thrown from the top of 36m high tower with velocity 5m/ss at an angle 37∘ above the horizontal as shown. Its horizontal distance on the ground is closest to [g=10m/s2
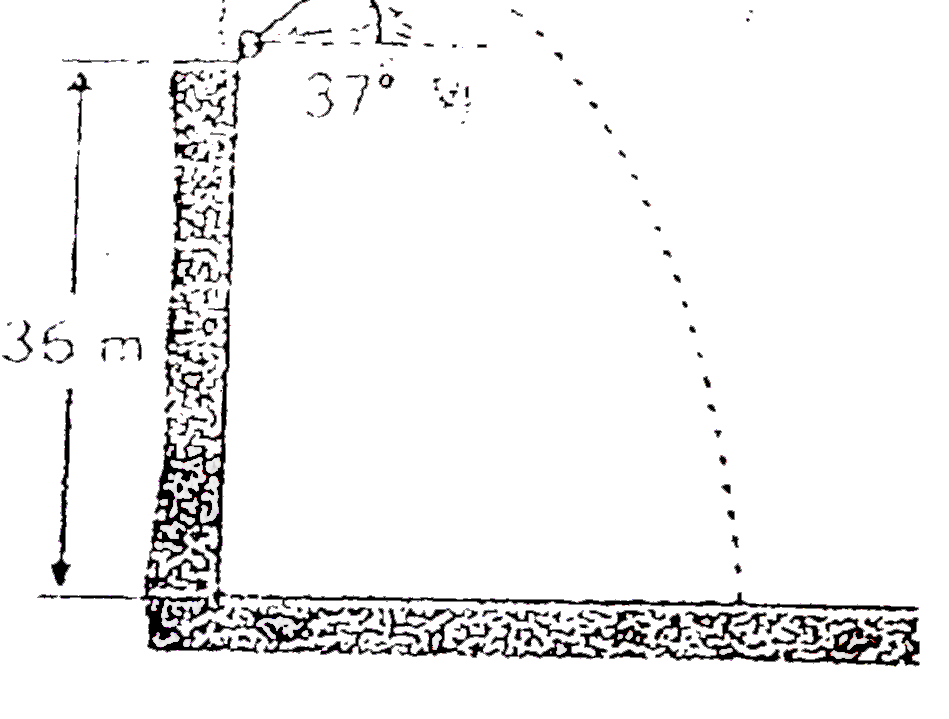 : A12mB18mC24mD30m
: A12mB18mC24mD30m
A particle is projected with a velocity 10 m//s at an angle 37∘ to the horizontal. Find the location at which the particle is at a height 1 m from point of projection.
View SolutionA ball is projected from the ground with speed u at an angle α with horizontal. It collides with a wall at a distance a from the point of projection and returns to its original position. Find the coefficient of restitution between the ball and the wall.
View SolutionA particle is projected with 40ms−1 at anlge 53∘ above horizontal. It speed when it is moving at 37∘ with horizontal is
View SolutionA paricle is projected from a point with initial speed of 10m/sec at an angle of 37∘ with the horizontal. At the same instant a fly starts on the same path of particle with constant speed of 10m/s Then :
View SolutionA stone is thrown with a speed of 10ms−1 at an angle of projection 60∘. Find its height above the point of projection when it is at a horizontal distance of 3m from the thrower ? (Take g=10ms−2)
View Solution
