The relation between length L and radius R of the cylinder , if its moment of inertia about its axis is equal to that about the equatorial axis, will be
L = R
L = 2R
L = 3R
L=√3R
The correct Answer is:D
To solve the problem, we need to find the relationship between the length L and the radius R of a cylinder when its moment of inertia about its axis is equal to that about its equatorial axis.
1. Identify the Moments of Inertia:
- The moment of inertia of a solid cylinder about its own axis (longitudinal axis) is given by:
I1=12mR2
- The moment of inertia about the equatorial axis (perpendicular to the length of the cylinder) can be calculated using the parallel axis theorem. The moment of inertia about the equatorial axis is:
I2=112mL2+m(L2)2
Simplifying this gives:
I2=112mL2+14mL2=(112+312)mL2=13mL2
2. Set the Moments of Inertia Equal:
- According to the problem, we have:
I1=I2
- Substituting the expressions we derived:
12mR2=13mL2
3. Cancel the Mass:
- Since mass m appears on both sides, we can cancel it out:
12R2=13L2
4. Cross-Multiply to Solve for L and R:
- Cross-multiplying gives:
3R2=2L2
5. Rearranging the Equation:
- Rearranging the equation to express L in terms of R:
L2=32R2
- Taking the square root of both sides:
L=R√32=R√62
6. Final Relationship:
- Therefore, the relationship between the length L and the radius R of the cylinder is:
L=√62R
- The moment of inertia of a solid cylinder about its own axis (longitudinal axis) is given by:
I1=12mR2
- The moment of inertia about the equatorial axis (perpendicular to the length of the cylinder) can be calculated using the parallel axis theorem. The moment of inertia about the equatorial axis is:
I2=112mL2+m(L2)2
Simplifying this gives:
I2=112mL2+14mL2=(112+312)mL2=13mL2
- According to the problem, we have:
I1=I2
- Substituting the expressions we derived:
12mR2=13mL2
- Since mass m appears on both sides, we can cancel it out:
12R2=13L2
- Cross-multiplying gives:
3R2=2L2
- Rearranging the equation to express L in terms of R:
L2=32R2
- Taking the square root of both sides:
L=R√32=R√62
- Therefore, the relationship between the length L and the radius R of the cylinder is:
L=√62R
Topper's Solved these Questions
Similar Questions
What must be the relation between length and radius of a cylinder of given mass and density so that its moment of inertia about an axis through its center of mass and perpendicular to its length may be minimum?
View SolutionA cylinder of 500 g and radius 10 cm has moment of inertia (about its natural axis)
View Solution
Knowledge Check
A thin wire of mass M and length L is turned into a ring. The moment of inertia about its axis will be:
A14π2ML2B112ML2C13π2ML2D1π2ML2A wire of mass m and length l is bent in the form of circular ring. The moment of inertia of the ring about its axis is
AMl4π2BMl2πCMl4πDMl24π2Moment of inertia of a hollow cylinder of mass M and radius r about its own axis is
A23Mr2BMr2C13Mr2D12Mr2
A uniform disc of radius R lies in xy plane with its centre at origin. Its moment of inertia about the axis x = 2 R and y =0 is equal to the moment of inertia about the axis y =d and z = 0. What is d equal to ?
View SolutionA thin wire of length l and mass m is turned into the form of a semicircle. Its moment of inertia about an axis joining its free ends will be
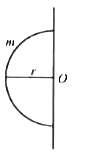
View SolutionThe moment f inertia of a solid cylinder about an axis parallel to its length and passing through its centre is equal to its moment of inertia about an axis perpendicular to the length of cylinder and passing through its centre . The ratio of radius of cylinder and its length is
View SolutionA circular disc of radius R and thickness r6 has moment of inertia I about its axis. If it is melted and casted into a solid sphere then what will be its moment of inertia, about its diametric axis?
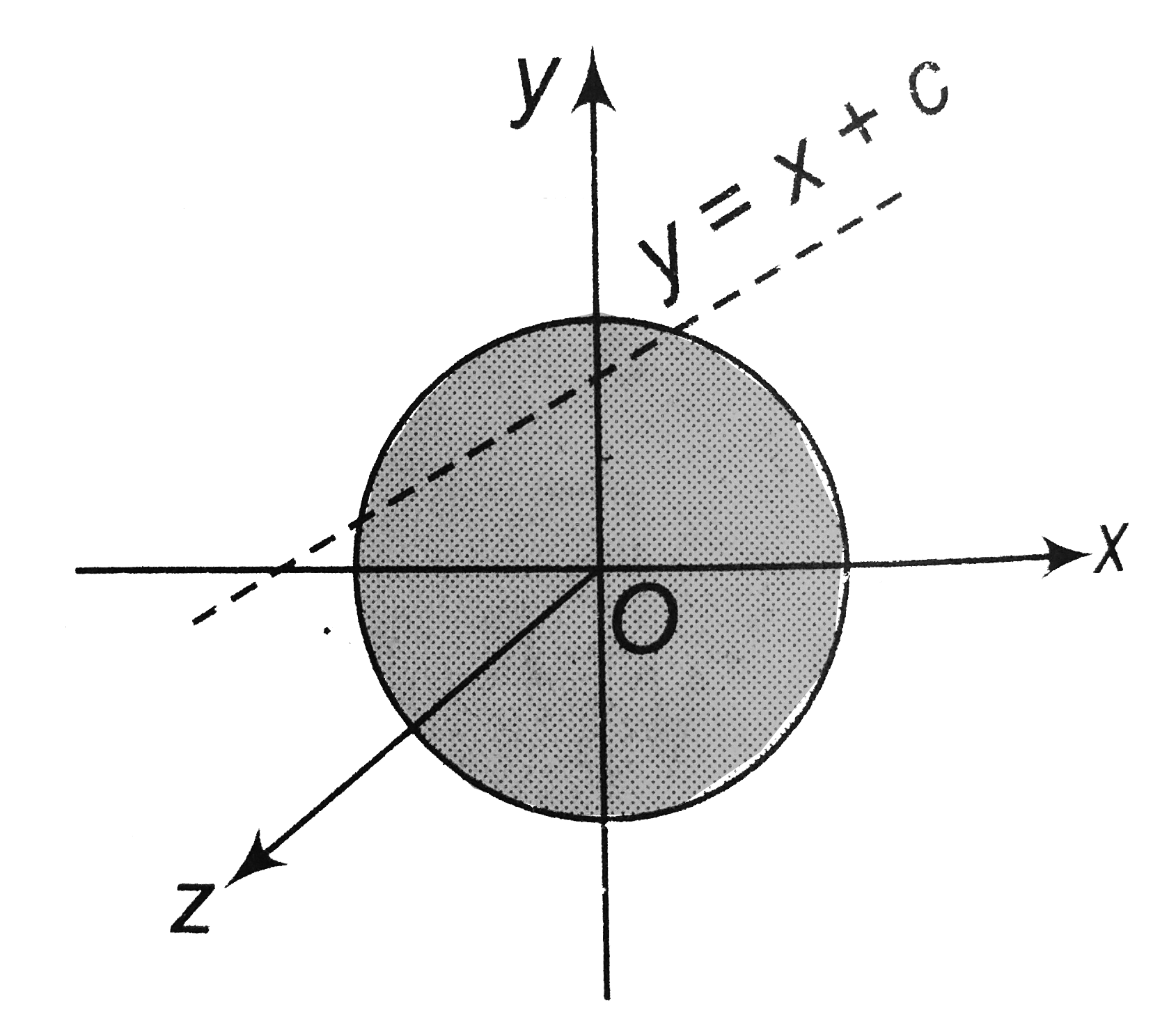
View SolutionA uniform disc of radius R lies in the x−y plane, with its centre at origin. Its moment of inertia about z-axis is equal to its moment of inertia about line y=x+c. The value of c will be.
 .
.
View Solution