A square plate is kept in YZ plane. Then according to perpendicular axis theorem
IZ=IX+IY
IX=IY+IZ
IY=IX+IZ
All of the above
The correct Answer is:B
To solve the problem regarding the perpendicular axis theorem for a square plate kept in the YZ plane, we will follow these steps:
1. Understanding the Geometry:
- We have a square plate lying in the YZ plane. The axes are defined as follows: Y-axis is vertical, and Z-axis is horizontal. The X-axis is perpendicular to the YZ plane.
2. Defining the Moment of Inertia:
- According to the perpendicular axis theorem, for a planar body (like our square plate), the moment of inertia about an axis perpendicular to the plane (X-axis) is equal to the sum of the moments of inertia about the two axes in the plane (Y-axis and Z-axis).
- Mathematically, this can be expressed as:
Ix=Iy+Iz
where:
- Ix is the moment of inertia about the X-axis,
- Iy is the moment of inertia about the Y-axis,
- Iz is the moment of inertia about the Z-axis.
3. Calculating the Moments of Inertia:
- For a square plate of mass m and side length a:
- The moment of inertia about the Y-axis (Iy) can be calculated as:
Iy=112ma2
- The moment of inertia about the Z-axis (Iz) can be calculated similarly:
Iz=112ma2
4. Applying the Perpendicular Axis Theorem:
- Substitute the values of Iy and Iz into the equation:
Ix=Iy+Iz=112ma2+112ma2=16ma2
5. Conclusion:
- Therefore, the relation according to the perpendicular axis theorem for the square plate in the YZ plane is:
Ix=Iy+Iz
- This confirms that the moment of inertia about the X-axis is equal to the sum of the moments of inertia about the Y and Z axes.
- We have a square plate lying in the YZ plane. The axes are defined as follows: Y-axis is vertical, and Z-axis is horizontal. The X-axis is perpendicular to the YZ plane.
- According to the perpendicular axis theorem, for a planar body (like our square plate), the moment of inertia about an axis perpendicular to the plane (X-axis) is equal to the sum of the moments of inertia about the two axes in the plane (Y-axis and Z-axis).
- Mathematically, this can be expressed as:
Ix=Iy+Iz
where:
- Ix is the moment of inertia about the X-axis,
- Iy is the moment of inertia about the Y-axis,
- Iz is the moment of inertia about the Z-axis.
- For a square plate of mass m and side length a:
- The moment of inertia about the Y-axis (Iy) can be calculated as:
Iy=112ma2
- The moment of inertia about the Z-axis (Iz) can be calculated similarly:
Iz=112ma2
- Substitute the values of Iy and Iz into the equation:
Ix=Iy+Iz=112ma2+112ma2=16ma2
- Therefore, the relation according to the perpendicular axis theorem for the square plate in the YZ plane is:
Ix=Iy+Iz
- This confirms that the moment of inertia about the X-axis is equal to the sum of the moments of inertia about the Y and Z axes.
Topper's Solved these Questions
Similar Questions
Knowledge Check
If a body is lying in the Y-Z plane, then according to theorem of perpendiculr axes the correct expression will be
AIz=Ix+IyBIy=Ix+IzCIx=Iy+IzDIy=Iz+Md2Consider a semicircular ring with mass m and radius R as shown in figure.
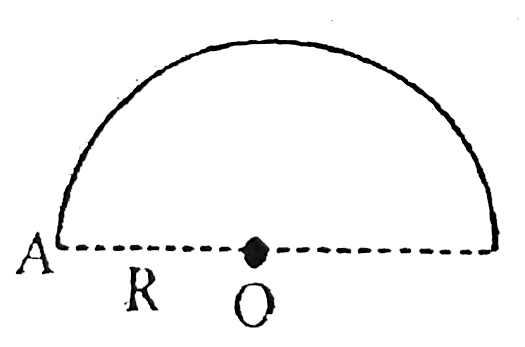
Statement-1: The moment of inertia of semi - circular ring about an axis passing through A and perpendicular to plane is 2mR2
Statement-2: According to parallel axis theorem: IA=1cm+mR2AStatement-1 is true, statement-2 is true and statement-2 is correct explanation for statement-1.BStatement-1 is true, statement-2 is true and statement-2 is NOT the correct explanation for statement-1.CStatement-1 is true, statement-2 is false.DStatement -1 is false, statement -2 is true.According to de morgan's theorem-
A¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯A+B+C=¯¯¯A+¯¯¯B+¯¯¯CB¯¯¯¯¯¯¯¯¯ABC=¯¯¯¯¯¯¯¯¯ABCC¯¯¯¯¯¯¯¯¯ABC=¯¯¯A+¯¯¯B+¯¯¯CD¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯A+B+C=ABC
A square plate of side a is placed in xy plane having centre at origin if charge at density of square plate is σ=xy then total charge on the plate will be
View SolutionMoment of inertia of a square plate of side l about the axis passing through one of the corner and perpendicular to the plane of square plate is given by :
View SolutionMoment of Inertia of bodies: rod | Ring | Disc| Sheet | Sphere| Parallel axis and perpendicular axis theorem
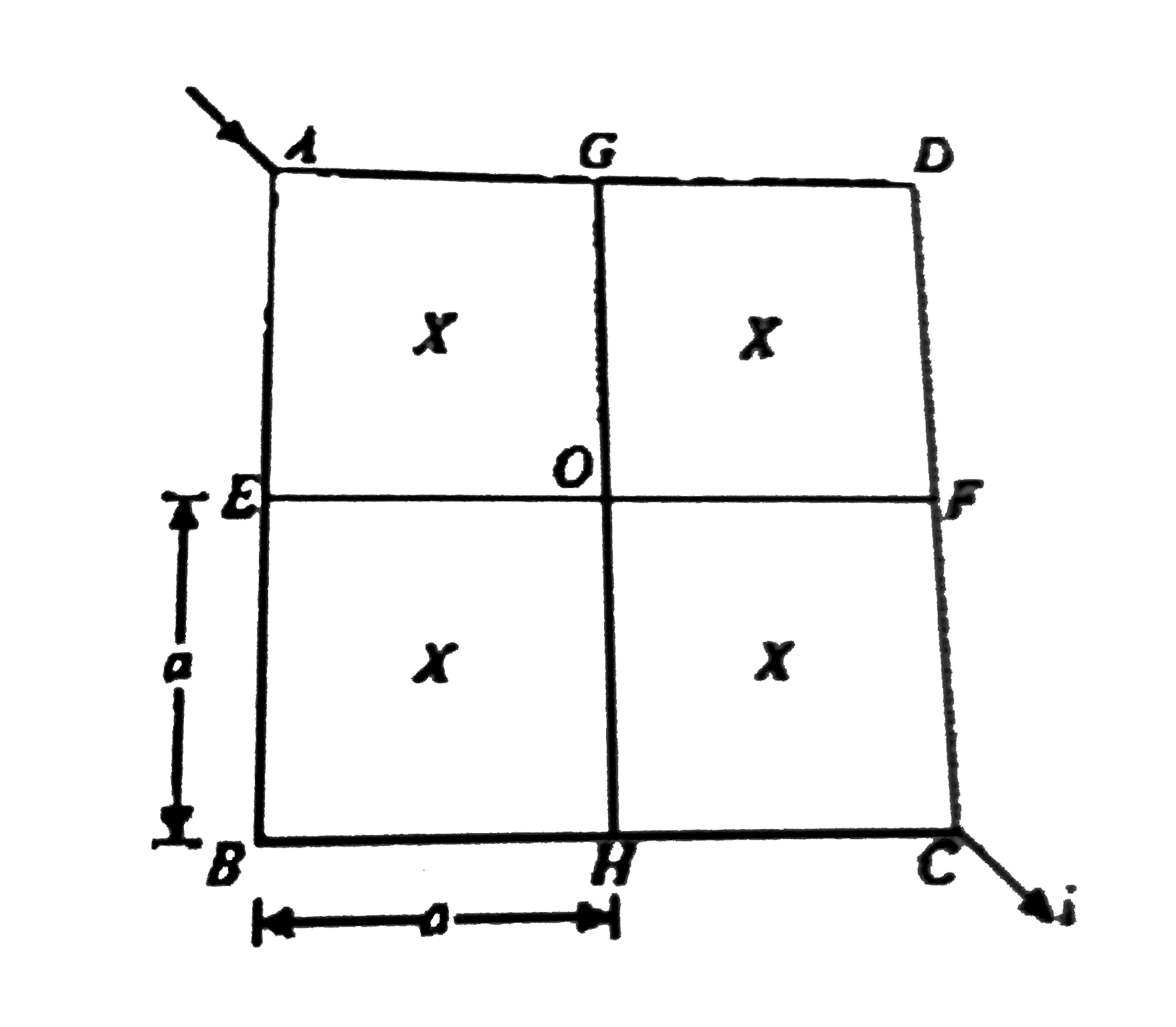
View SolutionThe figure-4.240 shows ·a square wire mesh made of conducting wires. Here, each small square has side a. The structure is kept in uniform magnetic field B perpendicular to the plane of paper:
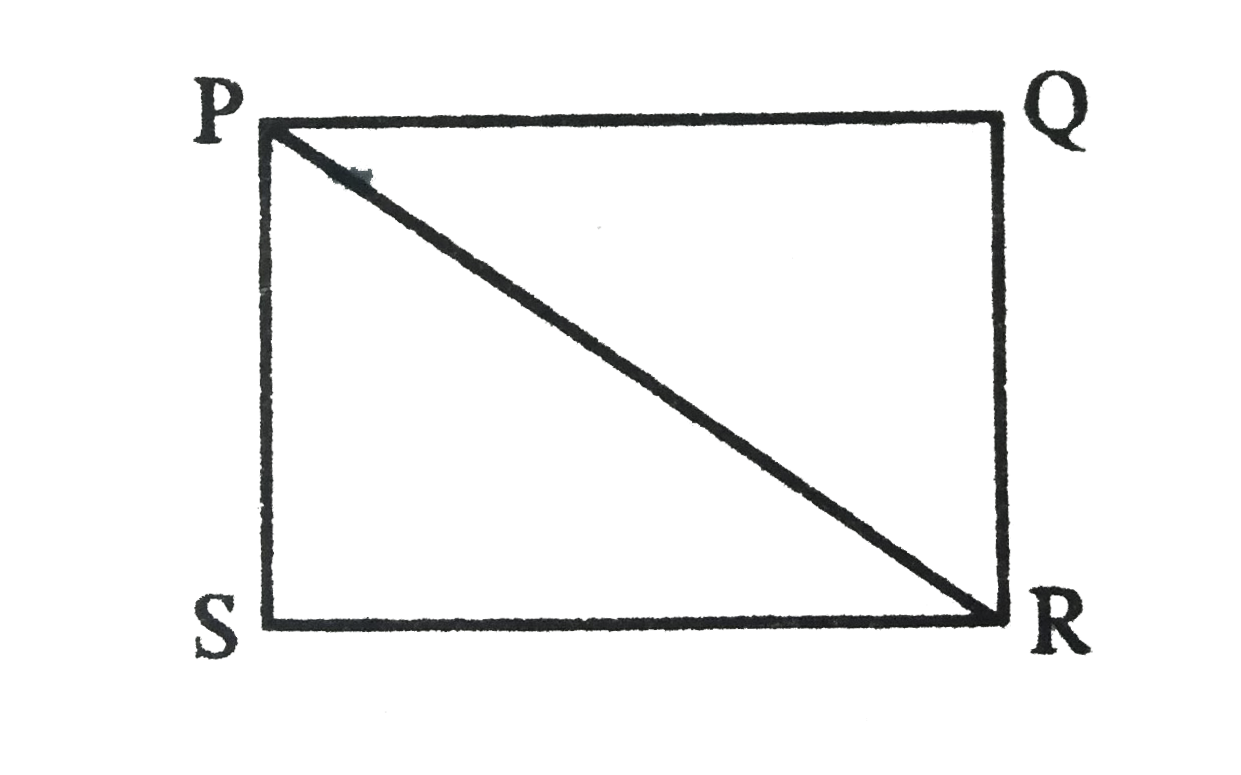
View SolutionMoment of inertia of a rectangular plate about an axis passing through P and perpendicular to the plate is I. Moment of PQR about an axis perpendicular to the plane of the plate :
 .
.
View Solution
