Two particles of mass m and 2m have their position vectors as a function of time as r1(t)=ˆi−t3ˆj+2t2ˆkandr2(t)=tˆi−t3ˆj−t2ˆk respectively (where t is the time). Which one of the following graphs represents the path of the centre of mass ?
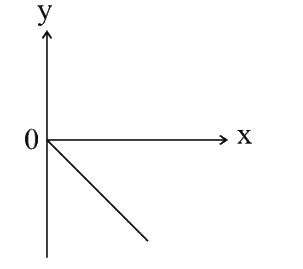
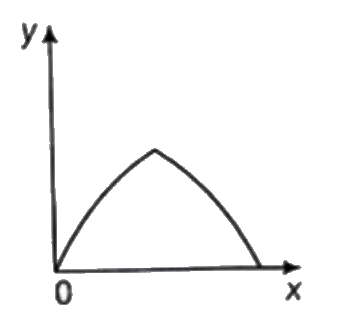
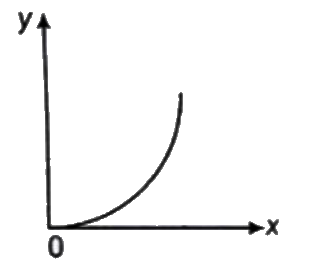
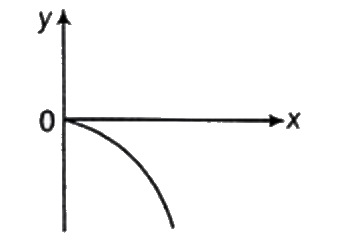
The correct Answer is:D
To find the path of the center of mass of two particles with given position vectors, we can follow these steps:
Step 1: Identify the position vectors
The position vectors of the two particles are given as:
- For particle 1 (mass m):
→r1(t)=^i−t3^j+2t2^k
- For particle 2 (mass 2m):
→r2(t)=t^i−t3^j−t2^k
Step 2: Write the formula for the center of mass
The position vector of the center of mass →rcm for two particles can be calculated using the formula:
→rcm=m1→r1+m2→r2m1+m2
Where:
- m1=m (mass of particle 1)
- m2=2m (mass of particle 2)
Step 3: Substitute the values into the formula
Substituting the masses and position vectors into the formula:
→rcm=m→r1+2m→r2m+2m
This simplifies to:
→rcm=m→r1+2m→r23m
→rcm=13(→r1+2→r2)
Step 4: Calculate →rcm
Now, we will calculate →rcm:
→rcm=13((^i−t3^j+2t2^k)+2(t^i−t3^j−t2^k))
Expanding this:
=13(^i−t3^j+2t2^k+2t^i−2t3^j−2t2^k)
Combining like terms:
=13((1+2t)^i+(−1−2)t3^j+(2−2)t2^k)
This simplifies to:
=13((1+2t)^i−3t3^j)
Step 5: Write the final expression for →rcm
Thus, the position vector of the center of mass is:
→rcm=1+2t3^i−t3^j
Step 6: Analyze the components
From the expression:
- The x-component is 1+2t3 which is always positive for t≥0.
- The y-component is −t3 which is always negative for t>0.
Step 7: Determine the path
The path of the center of mass will be a curve where:
- As t increases, the x-coordinate increases linearly, while the y-coordinate decreases cubically.
Conclusion
Based on the analysis, the graph representing the path of the center of mass will show a positive x-coordinate and a negative y-coordinate, indicating a curve that moves upwards to the right and downwards in the y-direction.
The position vectors of the two particles are given as:
- For particle 1 (mass m):
→r1(t)=^i−t3^j+2t2^k
- For particle 2 (mass 2m):
→r2(t)=t^i−t3^j−t2^k
The position vector of the center of mass →rcm for two particles can be calculated using the formula:
→rcm=m1→r1+m2→r2m1+m2
Where:
- m1=m (mass of particle 1)
- m2=2m (mass of particle 2)
Substituting the masses and position vectors into the formula:
→rcm=m→r1+2m→r2m+2m
This simplifies to:
→rcm=m→r1+2m→r23m
→rcm=13(→r1+2→r2)
Now, we will calculate →rcm:
→rcm=13((^i−t3^j+2t2^k)+2(t^i−t3^j−t2^k))
Expanding this:
=13(^i−t3^j+2t2^k+2t^i−2t3^j−2t2^k)
Combining like terms:
=13((1+2t)^i+(−1−2)t3^j+(2−2)t2^k)
This simplifies to:
=13((1+2t)^i−3t3^j)
Thus, the position vector of the center of mass is:
→rcm=1+2t3^i−t3^j
From the expression:
- The x-component is 1+2t3 which is always positive for t≥0.
- The y-component is −t3 which is always negative for t>0.
The path of the center of mass will be a curve where:
- As t increases, the x-coordinate increases linearly, while the y-coordinate decreases cubically.
Based on the analysis, the graph representing the path of the center of mass will show a positive x-coordinate and a negative y-coordinate, indicating a curve that moves upwards to the right and downwards in the y-direction.
Topper's Solved these Questions
Similar Questions
Knowledge Check
The position vectors of three particles of mass m1=1kg,m2=2kgandm3=3kg are r1=(ˆi+4ˆj+ˆk)m, r2=(ˆi+ˆj+ˆk)m and r3=(2ˆi−ˆj−ˆ2k)m, respectively. Find the position vector of their center of mass.
Arcm=12(3i+j−2k)mBrcm=12(3i+2j−k)mCrcm=12(3i+3j−k)mDrcm=12(3i+j−k)mTwo particles of mass 1kgand3kg have position vectors 2ˆi+3ˆj+4ˆkand−2ˆi+3ˆj−4ˆk respectively. The centre of mass has a position vector.
Aˆi+3ˆj−2ˆkB−ˆi−3ˆj−2ˆkC−ˆi+3ˆj+2ˆkD−ˆi+3ˆj−2ˆkFind the area of triangle if position vector of vertices w.r.t. O is −ˆi+2ˆj+3ˆk,2ˆi−ˆj−ˆk,ˆi+ˆj−ˆk.
A√892sq.unitsB892sq.unitsC2√79sq.unitsD792sq.units
The position vector of a particle changes with time according to the relation →r(t)=15t2ˆi+(4−20t2)ˆj What is the magnitude of the acceleration at t = 1?
View SolutionTwo blocks of mass 1kg and 3kg have position v ectors ˆi+2ˆj+ˆk and 3ˆi−2ˆj+ˆk , respectively . The center of mass of this system has a position vector.
View SolutionIf A(1,1,1),C(2,−1,2) the vector equation of the line −−→AB is →r=(ˆi+ˆj+ˆk)+t(6ˆi−3ˆj+2ˆk) and d is the shrotest distance of the point C form −−→AC then
View SolutionThe position vector of the point, were the line r=ˆi−ˆj+ˆk+t(ˆi+ˆj−ˆk) meets the plane rc.ˆi+ˆj+ˆk=5 is
View SolutionThe time dependence of the position of a particle of mass m = 2 is given by →r(t)=2tˆi−3t2ˆj Its angular momentum, with respect to the origin, at time t = 2 is :
View Solution
