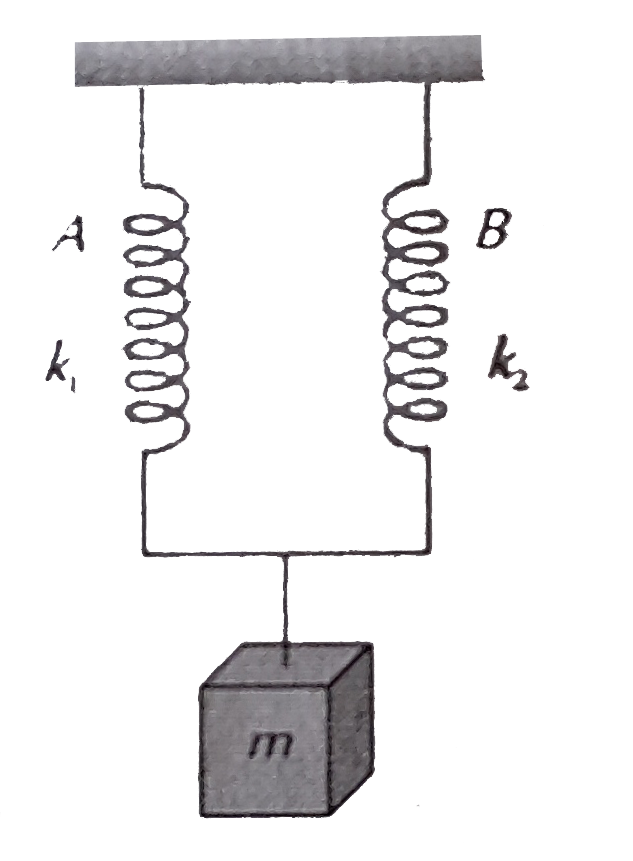
Two springs are joined and attached to a mass of 16 kg. The system is then suspended vertically from a rigid support. The spring constant of the two spring are $k_{1} and k_{2}$ respectively. The period of vertical oscillations of the system will be

$8 π \sqrt{\frac{k_{1} + k_{2}}{k_{1} k_{2}}}$

$\frac{π}{2} \sqrt{\frac{k_{1}}{k_{2}}}$

$\sqrt{\frac{k_{1} + k_{2}}{8 π}}$

$π \sqrt{\frac{k_{1} - k_{2}}{2}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Updated on:21/07/2023

Answer

Step by step video, text & image solution for Two springs are joined and attached to a mass of 16 kg. The system is then suspended vertically from a rigid support. The spring constant of the two spring are k_1 and k_2 respectively. The period of vertical oscillations of the system will be by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS NTA NEET SET 62

Topper's Solved these Questions

Knowledge Check

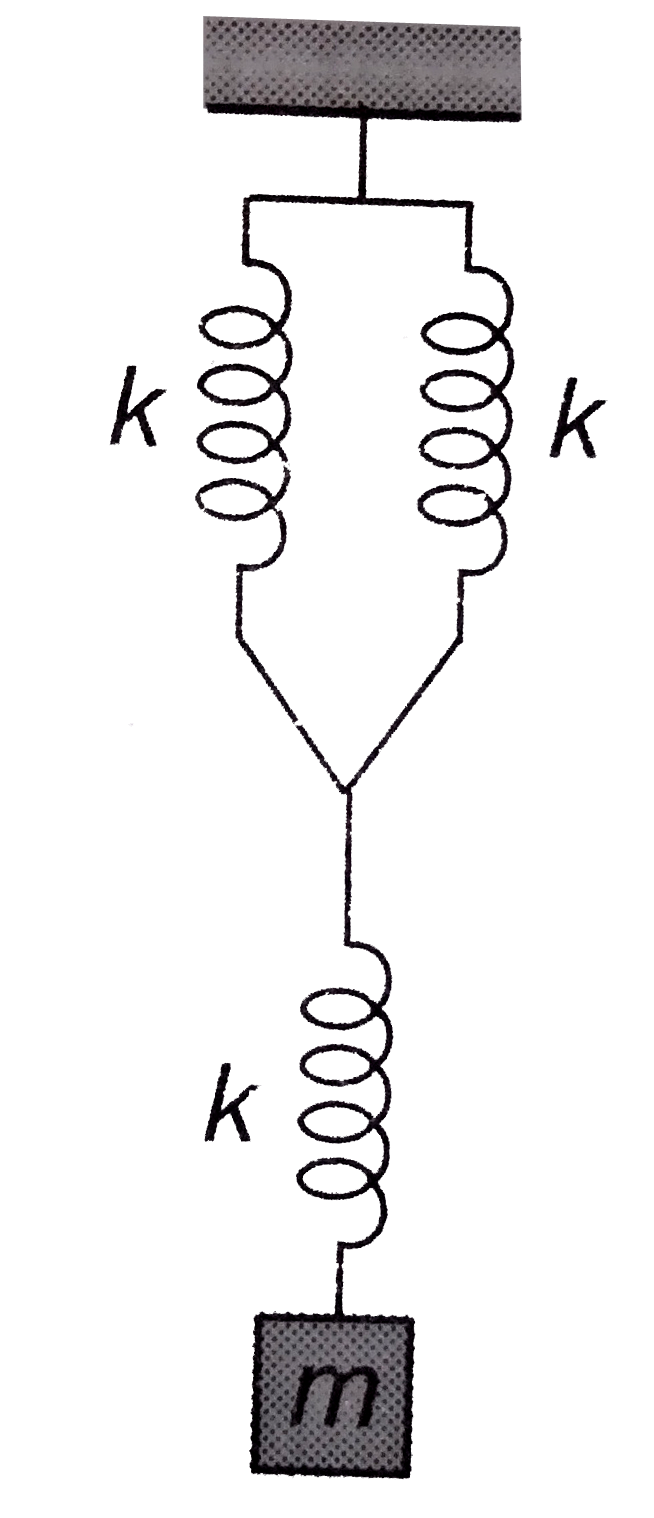
A particle of mass $m$ is attached to three identical springs of spring constant $k$ as shwon in figure. The time period of vertical oscillation of the particle is

A $2 π \sqrt{\frac{m}{k}}$
B $2 π \sqrt{\frac{m}{2 k}}$
C $2 π \sqrt{\frac{m}{3 k}}$
D $π \sqrt{\frac{m}{k}}$
A particle of mass m is attached to three identical massless springs of spring constant k as shown in the m 135 figure. The time period of vertical oscillation of the particle is

A $2 π \sqrt{\frac{m}{k}}$
B $2 π \sqrt{\frac{m}{2 k}}$
C $2 π \sqrt{\frac{m}{3 k}}$
D $π \sqrt{\frac{m}{k}}$
A mass m is suspended by means of two coiled springs which have the same length in unstretched condition as shown in figure. Their force constants are $k_{1} and k_{2}$ respectively. When set into vertical vibrations, the period will be

A $2 π \sqrt{(\frac{m}{k_{1} k_{2}})}$
B $2 π \sqrt{m (\frac{k_{1}}{k_{2}})}$
C $2 π \sqrt{(\frac{m}{k_{1} - k_{2}})}$
D $2 π \sqrt{(\frac{m}{k_{1} + k_{2}})}$

NTA MOCK TESTS-NTA NEET SET 62-PHYSICS

Home
Ask Doubt
Profile

Two springs are joined and attached to a mass of 16 kg. The system is then suspended vertically from a rigid support. The spring constant of the two spring are k1andk2 respectively. The period of vertical oscillations of the system will be

The correct Answer is:A

Topper's Solved these Questions

Similar Questions

Knowledge Check

A particle of mass m is attached to three identical springs of spring constant k as shwon in figure. The time period of vertical oscillation of the particle is

A particle of mass m is attached to three identical massless springs of spring constant k as shown in the m 135 figure. The time period of vertical oscillation of the particle is

A mass m is suspended by means of two coiled springs which have the same length in unstretched condition as shown in figure. Their force constants are k1andk2 respectively. When set into vertical vibrations, the period will be

NTA MOCK TESTS-NTA NEET SET 62-PHYSICS

Two springs are joined and attached to a mass of 16 kg. The system is then suspended vertically from a rigid support. The spring constant of the two spring are $k_{1} and k_{2}$ respectively. The period of vertical oscillations of the system will be

A particle of mass $m$ is attached to three identical springs of spring constant $k$ as shwon in figure. The time period of vertical oscillation of the particle is

A mass m is suspended by means of two coiled springs which have the same length in unstretched condition as shown in figure. Their force constants are $k_{1} and k_{2}$ respectively. When set into vertical vibrations, the period will be